
【题目】已知:直线 AB,CD 相交于点 O,且OE CD ,如图.
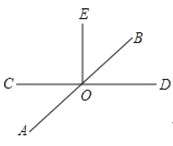
(1)过点 O 作直线 MN AB;
(2)若点 F 是(1)中所画直线 MN 上任意一点(O 点除外),且AOC 35°,求EOF的度数;
(3)若BOD:DOA 1:5,求AOE 的度数.
【答案】(1)见解析(2)35°或145°(3)120°
【解析】
(1)根据垂直的定义即可作图;
(2)分F在射线OM上和在射线ON上分别进行求解即可;
(3)依据平角的定义以及垂线的定义,即可得到∠AOE的度数.
(1)如图,MN为所求;
(2)若F在射线OM上,
∵MN AB,OE CD ,
∴∠AOC+∠COM=90°,∠EOF+∠COM =90°,
则∠EOF=∠AOC=35°;
若F'在射线ON上,
∵MN AB,OE CD ,
∴∠DON=∠COM=90°-∠AOC=55°,∠EOD=90°
则∠EOF'=∠DOE+∠DON=145°;
综上所述,∠EOF的度数为35°或145°;
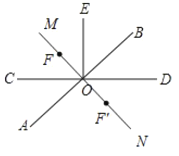
(3)∵BOD:DOA 1:5
∴∠BOD:∠BOC=1:5,
∴∠BOD=![]() ∠COD=30°,
∠COD=30°,
∴∠AOC=30°,
又∵EO⊥CD,
∴∠COE=90°,
∴∠AOE=90°+30°=120°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, BM切⊙O于点B,点P是⊙O上的一个动点(不经过A,B两点),过O作OQ∥AP交![]() 于点Q,过点P作
于点Q,过点P作![]() 于C,交
于C,交![]() 的延长线于点E,连结
的延长线于点E,连结![]() .
.
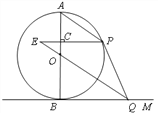
(1)求证:PQ与⊙O相切;
(2)若直径AB的长为12,PC=2EC,求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
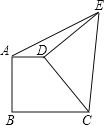
A. 1 B. 2 C. 3 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国七十周年,南岗区准备对某道路工程进行改造,若请甲工程队单独做此工程需4个月完成,若请乙工程队单独做此工程需6个月完成,若甲、乙两队合作2个月后,甲工程队到期撤离,则乙工程队再单独需几个月能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形AOCD的顶点A、C分别在y轴和x轴上,点P的坐标为(2,0),以点P为圆心,OP的长为半径向正方形内部作一半圆,交线段DF于点F,线段DF的延长线交y轴于点E,DF=DC.
(1)求证:DF是半圆P的切线;
(2)求线段DF所在直线的解析式;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为![]() 轴、
轴、![]() 轴的正方向建立平面直角坐标系,有如下四个结论:
轴的正方向建立平面直角坐标系,有如下四个结论:
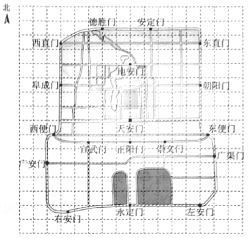
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(![]() ,
,![]() )时,表示左安门的点的坐标为(5,
)时,表示左安门的点的坐标为(5,![]() );
);
②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(![]() ,
,![]() )时,表示左安门的点的坐标为(10,
)时,表示左安门的点的坐标为(10,![]() );
);
③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(![]() ,
,![]() )时,表示左安门的点的坐标为(
)时,表示左安门的点的坐标为(![]() ,
,![]() );
);
④当表示天安门的点的坐标为(![]() ,
,![]() ),表示广安门的点的坐标为(
),表示广安门的点的坐标为(![]() ,
,![]() )时,表示左安门的点的坐标为(
)时,表示左安门的点的坐标为(![]() ,
,![]() ).
).
上述结论中,所有正确结论的序号是
A. ①②③ B. ②③④ C. ①④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
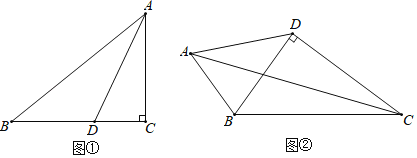
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com