
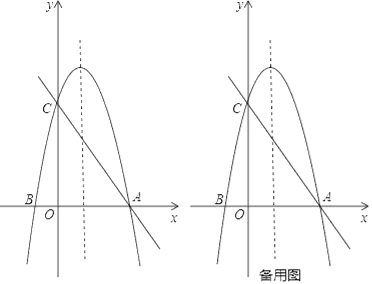
【题目】如图,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A,点B(﹣1,0),与y轴交于点C(0,4),作直线AC.
(1)求抛物线解析式;
(2)点P在抛物线的对称轴上,且到直线AC和x轴的距离相等,设点P的纵坐标为m,求m的值;
(3)点M在y轴上且位于点C上方,点N在直线AC上,点Q为第一象限内抛物线上一点,若以点C、M、N、Q为顶点的四边形是菱形,请直接写出点Q的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)m的值为1或﹣4;(3)点Q的坐标为(1,
x+4;(2)m的值为1或﹣4;(3)点Q的坐标为(1,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先利用抛物线的对称性得到A(3,0),则可设交点式y=a(x+1)(x﹣3),然后把C点坐标代入求出a即可;
(2)先利用待定系数法其出直线AC的解析式为y=﹣![]() x+4;令对称轴与直线AC交于点D,与x轴交于点E,作PH⊥AD于H,如图1,易得D(1,
x+4;令对称轴与直线AC交于点D,与x轴交于点E,作PH⊥AD于H,如图1,易得D(1,![]() ),利用勾股定理计算出AD=
),利用勾股定理计算出AD=![]() ,设P(1,m),则PD=
,设P(1,m),则PD=![]() ﹣m,PH=PE=|m|,证明△DPH∽△DAE,利用相似比得到
﹣m,PH=PE=|m|,证明△DPH∽△DAE,利用相似比得到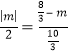 ,然后解方程可得到m的值;
,然后解方程可得到m的值;
(3)设Q(t,﹣![]() x2+
x2+![]() x+4)(0<t<4),讨论:当CM为对角线时,四边形CQMN为菱形,如图2,根据菱形的性质判定点N和Q关于y轴对称,则N(﹣t,﹣
x+4)(0<t<4),讨论:当CM为对角线时,四边形CQMN为菱形,如图2,根据菱形的性质判定点N和Q关于y轴对称,则N(﹣t,﹣![]() x2+
x2+![]() x+4),然后把N(﹣t,﹣
x+4),然后把N(﹣t,﹣![]() x2+
x2+![]() x+4)代入y=﹣
x+4)代入y=﹣![]() x+4得t的方程,从而解方程求出t得到此时Q点坐标;当CM为菱形的边时,四边形CNQM为菱形,如图3,利用菱形的性质得NQ∥y轴,NQ=NC,则N(t,﹣
x+4得t的方程,从而解方程求出t得到此时Q点坐标;当CM为菱形的边时,四边形CNQM为菱形,如图3,利用菱形的性质得NQ∥y轴,NQ=NC,则N(t,﹣![]() t+4),所以NQ=﹣
t+4),所以NQ=﹣![]() t2+4t,再根据两点间的距离公式计算出CN=
t2+4t,再根据两点间的距离公式计算出CN=![]() t,所以﹣
t,所以﹣![]() t2+4t=
t2+4t=![]() t,从而解方程求出t得到此时Q点坐标.
t,从而解方程求出t得到此时Q点坐标.
解:(1)∵点A与点B(﹣1,0)关于直线x=1对称,
∴A(3,0),
设抛物线解析式为y=a(x+1)(x﹣3),
把C(0,4)代入得a1(﹣3)=4,解得a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() (x+1)(x﹣3),即y=﹣
(x+1)(x﹣3),即y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)设直线AC的解析式为y=kx+p,
把A(3,0),C(0,4)代入得![]() ,解得
,解得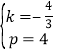 ,
,
∴直线AC的解析式为y=﹣![]() x+4;
x+4;
令对称轴与直线AC交于点D,与x轴交于点E,作PH⊥AD于H,如图1,
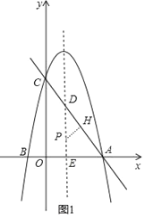
当x=1时,y=﹣![]() x+4=
x+4=![]() ,则D(1,
,则D(1,![]() ),
),
∴DE=![]() ,
,
在Rt△ADE中,AD=![]() =
=![]() ,
,
设P(1,m),则PD=![]() ﹣m,PH=PE=|m|,
﹣m,PH=PE=|m|,
∵∠PDH=∠ADE,
∴△DPH∽△DAE,
∴![]() ,即
,即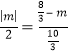 ,解得m=1或m=﹣4,
,解得m=1或m=﹣4,
即m的值为1或﹣4;
(3)设Q(t,﹣![]() t2+
t2+![]() t+4)(0<t<4),
t+4)(0<t<4),
当CM为对角线时,四边形CQMN为菱形,如图2,则点N和Q关于y轴对称,
∴N(﹣t,﹣![]() t2+
t2+![]() t+4),
t+4),
把N(﹣t,﹣![]() t2+
t2+![]() t+4)代入y=﹣
t+4)代入y=﹣![]() x+4得
x+4得![]() t+4=﹣
t+4=﹣![]() t2+
t2+![]() t+4,解得t1=0(舍去),t2=1,此时Q点坐标为(1,
t+4,解得t1=0(舍去),t2=1,此时Q点坐标为(1,![]() );
);
当CM为菱形的边时,四边形CNQM为菱形,如图3,则NQ∥y轴,NQ=NC,
∴N(t,﹣![]() t+4),
t+4),
∴NQ=﹣![]() t2+
t2+![]() t+4﹣(﹣
t+4﹣(﹣![]() t+4)=﹣
t+4)=﹣![]() t2+4t,
t2+4t,
而CN2=t2+(﹣![]() t+4﹣4)2=
t+4﹣4)2=![]() t2,即CN=
t2,即CN=![]() t,
t,
∴﹣![]() t2+4t=
t2+4t=![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,此时Q点坐标为(
,此时Q点坐标为(![]() ,
,![]() ),
),
综上所述,点Q的坐标为(1,![]() )或(
)或(![]() ,
,![]() ).
).


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
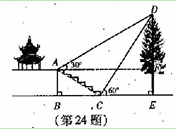
【题目】(本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为![]() (即AB:BC=
(即AB:BC=![]() ),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
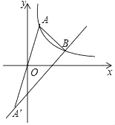
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1=![]() (x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(1)设a=2,点B(4,2)在函数y1,y2的图象上.
①分别求函数y1,y2的表达式;
②直接写出使y1>y2>0成立的x的范围.
(2)如图,设函数y1,y2的图象相交于点B,点B的横坐标为3a,△AA′B的面积为16,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
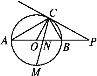
【题目】如图,AB是☉O的直径,点C在☉O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.
(1)求证:PC是☉O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若MN·MC=8,求☉O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
(3)当每斤的售价定为多少元时,每天获利最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 ;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣2x2+bx+c的图象经过点A(0,4)和B(1,﹣2).
(1)求此抛物线的解析式;
(2)求此抛物线的对称轴和顶点坐标;
(3)设抛物线的顶点为C,试求△CAO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B,E是半圆弧的三等分点,弧AB的长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )

A. 6![]() ﹣
﹣![]() B. 9
B. 9![]() ﹣
﹣![]() C.
C. ![]() ﹣
﹣![]() D. 6
D. 6![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
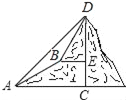
【题目】已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com