
【题目】如图,AB是☉O的直径,点C在☉O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.
(1)求证:PC是☉O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若MN·MC=8,求☉O的直径.
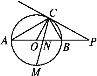
【答案】(1)由题意得到半径OC⊥PC, ∴PC是⊙O的切线(2)AB=4
【解析】
试题分析(1):因为同圆中半径相等,得到相等的角,直径所对的圆周角为90°,再由已知,经过等量代换,半径与直线垂直。(2)连接AM,BM.由题意易得△ANC∽△NMA,由已知一边的长为8,根据相似三角形的相似比求之。注意的是;相似比找准对应边。通过角找边容易。1)证明:∵OA=OC,
∴∠A=∠ACO.
∴∠COB=2∠ACO.
又∵∠COB=2∠PCB,
∴∠ACO =∠PCB. ........................................................ 1分
∵AB是⊙O的直径,
∴∠ACO +∠OCB="90" .
∴∠PCB +∠OCB="90," 即OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线. ………………………2分
(2)解:连接MA、MB.(如图)
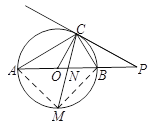
∵点M是弧AB的中点,
∴∠ACM=∠BAM.
∵∠AMC=∠AMN,
∴△AMC∽△NMA. …………………………3分
∴![]() .
.
∴![]() .
.
∵![]() =8,
=8,
∴![]() . ............................................................. 4分
. ............................................................. 4分
∵AB是⊙O的直径,点M是弧AB的中点,
∴∠AMB=90,AM=BM=![]() .
.
∴![]() . 5分
. 5分


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
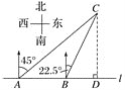
A. 2 km B. (2+![]() )km C. (4-2
)km C. (4-2![]() ) km D. (4-
) km D. (4-![]() ) km
) km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+![]() ,BC=2
,BC=2![]() ,求⊙O的半径.
,求⊙O的半径.
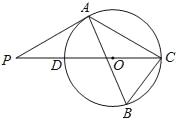
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:规定![]() 是任意一个两位及以上的自然数,将
是任意一个两位及以上的自然数,将![]() 的各位数字反向排列所得自然数
的各位数字反向排列所得自然数![]() 与
与![]() 相等,则称
相等,则称![]() 为回文数.如
为回文数.如![]() ,则称
,则称![]() 为回文数:如
为回文数:如![]() ,则
,则![]() 不是回文数.根据定义可得自然数列中11是第1个出现的回文数,则自然数列中第201个出现的回文数是__________.
不是回文数.根据定义可得自然数列中11是第1个出现的回文数,则自然数列中第201个出现的回文数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=1,AD=3,DC=5.点S沿A→B→C运动到C点停止,以S为圆心,SD为半径作弧交射线DC于T点,设S点运动的路径长为x,等腰△DST的面积为y,则y与x的函数图象应为( )
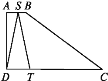
A. 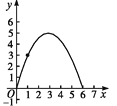 B.
B. 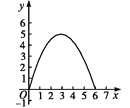
C. 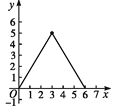 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
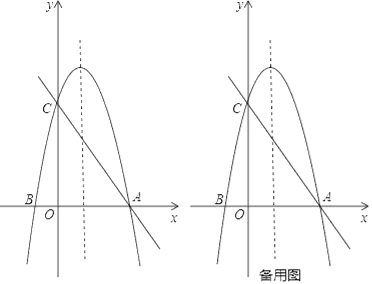
【题目】如图,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A,点B(﹣1,0),与y轴交于点C(0,4),作直线AC.
(1)求抛物线解析式;
(2)点P在抛物线的对称轴上,且到直线AC和x轴的距离相等,设点P的纵坐标为m,求m的值;
(3)点M在y轴上且位于点C上方,点N在直线AC上,点Q为第一象限内抛物线上一点,若以点C、M、N、Q为顶点的四边形是菱形,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
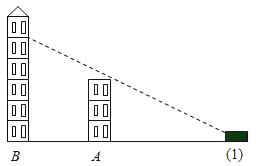
【题目】小明开着汽车在平坦的公路上行驶,前放出现两座建筑物A、B(如图),在(1)处小颖能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
(1)请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.
(2)若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com