
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
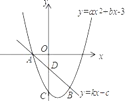
【答案】(1)y=x2﹣2x﹣3;(2)C(0,﹣3),D(0,﹣1);(3)P(1+![]() ,﹣2).
,﹣2).
【解析】
(1)把A(﹣1,0)、B(2,﹣3)两点坐标代入y=ax2+bx﹣3可得抛物线解析式.
(2)当x=0时可求C点坐标,求出直线AB解析式,当x=0可求D点坐标.
(3)由题意可知P点纵坐标为﹣2,代入抛物线解析式可求P点横坐标.
解:(1)把A(﹣1,0)、B(2,﹣3)两点坐标代入
y=ax2+bx﹣3可得 ![]()
解得![]()
∴y=x2﹣2x﹣3
(2)把x=0代入y=x2﹣2x﹣3中可得y=﹣3∴C(0,﹣3)
设y=kx+b,把A(﹣1,0)、B(2,﹣3)两点坐标代入
![]()
解得![]()
∴y=﹣x﹣1
∴D(0,﹣1)
(3)由C(0,﹣3),D(0,﹣1)可知CD的垂直平分线经过(0,﹣2)
∴P点纵坐标为﹣2,
∴x2﹣2x﹣3=﹣2
解得:x=1±![]() ,∵x>0∴x=1+
,∵x>0∴x=1+![]() .
.
∴P(1+![]() ,﹣2)
,﹣2)


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】在同一平面内,将两个全等的等腰直角三角形![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,若
,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合).
重合).
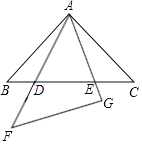
(1)求证:![]() ;
;
(2)在旋转过程中,试判断等式![]() 是否始终成立,若成立,请证明;若不成立,请说明理由.
是否始终成立,若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,平移一条抛物线,如果平移后的新抛物线经过原抛物线顶点,且新抛物线的对称轴是y轴,那么新抛物线称为原抛物线的“影子抛物线”.
中,平移一条抛物线,如果平移后的新抛物线经过原抛物线顶点,且新抛物线的对称轴是y轴,那么新抛物线称为原抛物线的“影子抛物线”.
(1)已知原抛物线表达式是![]() ,求它的“影子抛物线”的表达式;
,求它的“影子抛物线”的表达式;
(2)已知原抛物线经过点(1,0),且它的“影子抛物线”的表达式是![]() ,求原抛物线的表达式;
,求原抛物线的表达式;
(3)小明研究后提出:“如果两条不重合的抛物线交y轴于同一点,且它们有相同的“影子抛物线”,那么这两条抛物线的顶点一定关于y轴对称.”你认为这个结论成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
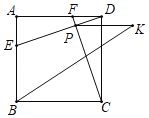
【题目】如图,正方形ABCD中,AB=4,E,F分别是边AB,AD上的动点,AE=DF,连接DE,CF交于点P,过点P作PK∥BC,且PK=2,若∠CBK的度数最大时,则BK长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是矩形;
(2)若E,F,G,H分别是OA,OB,OC,OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.
(1)若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是 ;
(2)若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷3枚硬币做游戏,其中1元硬币1枚,5角硬币两枚.
(1)求3枚硬币同时正面朝上的概率.
(2)小张、小王约定:正面朝上按面值算,背面朝上按0元算.3枚落地后,若面值和为1.5元,则小张获得1分;若面值和为1元,则小王得1分.谁先得到10分,谁获胜,请问这个游戏是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有任意三角形,当这个三角形的一条边上的中线等于这条边的一半时,称这个三角形叫“和谐三角形”,这条边叫“和谐边”,这条中线的长度叫“和谐距离”.
(1)已知A(2,0),B(0,4),C(1,2),D(4,1),这个点中,能与点O组成“和谐三角形”的点是 ,“和谐距离”是 ;
(2)连接BD,点M,N是BD上任意两个动点(点M,N不重合),点E是平面内任意一点,△EMN是以MN为“和谐边”的“和谐三角形”,求点E的横坐标t的取值范围;
(3)已知⊙O的半径为2,点P是⊙O上的一动点,点Q是平面内任意一点,△OPQ是“和谐三角形”,且“和谐距离”是2,请描述出点Q所在位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com