
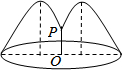
 如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为3米.
如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为3米.  轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
下列4对数值中是方程2x﹣y=1的解的是( )
A. 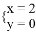 B.
B. 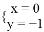 C.
C. 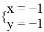 D.
D. 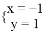
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
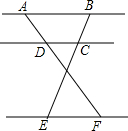 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AD}{DF}$=$\frac{BC}{CE}$ | B. | $\frac{BC}{CE}$=$\frac{DF}{AD}$ | C. | $\frac{CD}{EF}$=$\frac{BC}{BE}$ | D. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 小麦 | 玉米 | 黄豆 | |
| 亩产量(千克) | 600 | 900 | 330 |
| 销售单价(元/千克) | 2 | 1 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≠-$\frac{3}{2}$,n≠2 | B. | m≠-$\frac{3}{2}$,n=2 | C. | m=-$\frac{3}{2}$,n≠2 | D. | m=-$\frac{3}{2}$,n=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com