
分析 先利用二次函数的性质求出抛物线的对称轴为直线x=b,则当x>b时,y的值随x值的增大而减小,由于x>1时,y的值随x值的增大而减小,于是得到b≤1.
解答 解:抛物线的对称轴为直线x=-$\frac{b}{2×(-1)}$=$\frac{1}{2}$b,
因为a=-1<0,
所以抛物线开口向下,
所以当x>$\frac{1}{2}$b时,y的值随x值的增大而减小,
而2<x<5时,y随x的增大而减小,
所以$\frac{1}{2}$b≤2.
所以b≤4.
故答案为b≤4.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.


科目:初中数学 来源: 题型:解答题
 北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 价格x (元/个) | … | 30 | 50 | … |
| 销售量y (万个) | … | 5 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{3}$($\sqrt{3}$-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
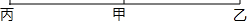 甲、乙、丙三地位置如图所示,甲、乙两地相距30km,丙地离甲地足够远,小明骑自行车从甲地往丙地,小军骑自行车从乙地往丙地,小明的速度为5km/h,小军的速度为15km/h.问:两人同时出发多长时间后相距20km?
甲、乙、丙三地位置如图所示,甲、乙两地相距30km,丙地离甲地足够远,小明骑自行车从甲地往丙地,小军骑自行车从乙地往丙地,小明的速度为5km/h,小军的速度为15km/h.问:两人同时出发多长时间后相距20km?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com