
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]()
⑴说明该方程根的情况.
⑵若![]() (
(![]() 为整数),且方程有两个整数根,求
为整数),且方程有两个整数根,求![]() 的值.
的值.
【答案】(1)见详解;(2)12
【解析】
(1)先计算判别式的值得到△=4(m-3)2-4(m2-8m+8),化简后得到△=8m+4,再根据8m+4的正负性即可判断方程根的情况;
(2)由于4<m<24且m为整数,则根据求根公式得到2m+1为完全平方数时,方程可能有整数根,则2m+1=16或25或36,再根据m为整数可求得m=12时,方程有两个整数根.
(1)解:∵a=1,b=-2(m-3),c=m2-8m+8,
∴△=4(m-3)2-4(m2-8m+8)
=8m+4,
当8m+4>0时,m>![]() ,此时方程有两个不相等的实数根,
,此时方程有两个不相等的实数根,
当8m+4=0时,m=![]() ,此时方程有两个相等的实数根,
,此时方程有两个相等的实数根,
当8m+4<0时,m<![]() ,此时方程没有实数根;
,此时方程没有实数根;
(2)解:∵a=1,b=-2(m-3),c=m2-8m+8,△=8m+4,
∴![]()
![]()
![]()
∵方程有两个整数根,
∴2m+1为完全平方数
∵4<m<24,
∴9<2m+1<49,
∴2m+1=16或25或36,
∴m=7.5或12或17.5,
又∵m为整数,
∴m=12.


科目:初中数学 来源: 题型:
【题目】如图,两个等腰直角三角形△ABC和△CDE中,∠ACB=∠DCE=90°,AB=13![]() ,CD=5
,CD=5![]() ,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.
,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(m+2)x+2m-1=0.
(1)求证方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图1,在平面直角坐标系中,点![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 是菱形,直线
是菱形,直线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

(1)点![]() 的坐标是______;
的坐标是______;
(2)求直线![]() 的函数解析式;
的函数解析式;
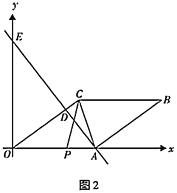
(3)如图2,动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位长度/秒的速度向终点
方向以1个单位长度/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式(要求写出自变量
之间的函数关系式(要求写出自变量![]() 的取值范围)
的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表:
输入汉字个数(个) | 132 | 133 | 134 | 135 | 136 | 137 | ||
甲班人数人) | 1 | 0 | 2 | 4 | 1 | 2 | ||
乙班人数(人) | 0 | 1 | 4 | 1 | 2 | 2 | ||
请分别判断下列同学是说法是否正确,并说明理由.
(1)两个班级输入汉字个数的平均数相同;
(2)两个班学生输入汉字的中位数相同众数也相同;
(3)甲班学生比乙班学生的成绩稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() .
.
(1)如图,点![]() 在
在![]() 延长线上,
延长线上,![]() ,求证:点
,求证:点![]() 为
为![]() 中点.
中点.

(2)如图,点![]() 在
在![]() 中点,
中点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() .
.
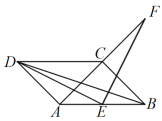
(3)在(2)的条件下,若![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,试判断四边形
,试判断四边形![]() 是否为平行四边形?并证明你的结论(先补全图形再解答).
是否为平行四边形?并证明你的结论(先补全图形再解答).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com