
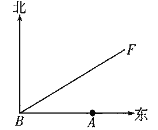
【题目】如图,A城气象台测得台风中心在A城正西方向320 km的B处,以每小时40 km的速度向北偏东60°的BF方向移动,距离台风中心200 km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
【答案】(1)A城受台风影响;(2)DA=200千米,AC=160千米
【解析】试题分析:(1)由A点向BF作垂线,垂足为C,根据勾股定理求得AC的长,与200比较即可得结论;(2)点A到直线BF的长为200千米的点有两点,分别设为D、G,则△ADG是等腰三角形,由于AC⊥BF,则C是DG的中点,在Rt△ADC中,解出CD的长,则可求DG长,在DG长的范围内都是受台风影响,再根据速度与距离的关系则可求时间.
试题解析:
(1)由A点向BF作垂线,垂足为C,
在Rt△ABC中,∠ABC=30°,AB=320km,则AC=160km,
因为160<200,所以A城要受台风影响;
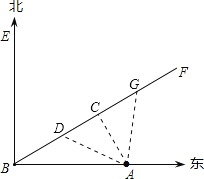
(2)设BF上点D,DA=200千米,则还有一点G,有AG=200千米.
因为DA=AG,所以△ADG是等腰三角形,
因为AC⊥BF,所以AC是DG的垂直平分线,CD=GC,
在Rt△ADC中,DA=200千米,AC=160千米,
由勾股定理得,CD=![]() =
=![]() =120千米,
=120千米,
则DG=2DC=240千米,
遭受台风影响的时间是:t=240÷40=6(小时).


科目:初中数学 来源: 题型:
【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
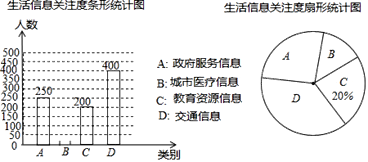
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 ![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( ) 
A.π+1
B.π+2
C.2π+2
D.4π+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度. 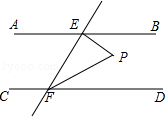
A.70
B.65
C.60
D.55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:

(1)这32名学生培训前考分的中位数所在的等级是 ,培训后考分的中位数所在的等级是 .
(2)这32名学生经过培训,考分等级“不合格” 的百分比由 下降到 .
(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有 名.
(4)你认为上述估计合理吗:理由是什么?
答: ,理由: .
查看答案和解析>>
科目:初中数学 来源: 题型:
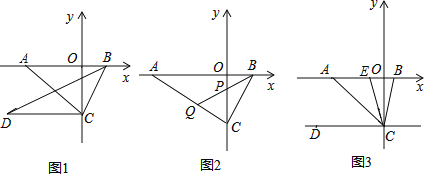
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,![]() ,
,![]() ,其中a、b满足关系式:
,其中a、b满足关系式:![]() .
.
![]() ______,
______,![]() ______,
______,![]() 的面积为______;
的面积为______;
![]() 如图2,石
如图2,石![]() 于点C,点P是线段OC上一点,连接BP,延长BP交AC于点
于点C,点P是线段OC上一点,连接BP,延长BP交AC于点![]() 当
当![]() 时,求证:BP平分
时,求证:BP平分![]() ;
;![]() 提示:三角形三个内角和等于
提示:三角形三个内角和等于![]()
![]() 如图3,若
如图3,若![]() ,点E是点A与点B之间上一点连接CE,且CB平分
,点E是点A与点B之间上一点连接CE,且CB平分![]() 问
问![]() 与
与![]() 有什么数量关系?请写出它们之间的数量关系并请说明理由.
有什么数量关系?请写出它们之间的数量关系并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com