
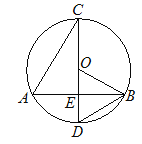
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
![]()
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.

(1)若当t的值为m时,PP′恰好经过点A,求m的值;
(2)设△P′PQ的面积为y,求y与t之间的函数关系式(m<t≤4) ;
(3)是否存在某一时刻t,使PQ平分角∠P′PC?存在,求相应的t值,不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高楼OB上有一旗杆CB,我校数学兴趣小组的同学准备利用所学的三角函数知识估测该高楼的高度,由于有其他建筑物遮挡视线不便测量,所以测量员沿坡度i=1:![]() 的山坡从坡脚的A处前行50米到达P处,测得旗杆顶部C的仰角为45°,旗杆底部B的仰角为37°(测量员的身高忽略不计),已知旗杆高BC=15米,则该高楼OB的高度为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
的山坡从坡脚的A处前行50米到达P处,测得旗杆顶部C的仰角为45°,旗杆底部B的仰角为37°(测量员的身高忽略不计),已知旗杆高BC=15米,则该高楼OB的高度为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. 45 B. 60 C. 70 D. 85
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )

A.128°B.118°C.108°D.98°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,∠C=90,BD是
ABC中,∠C=90,BD是![]() ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,

(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的边长为3,∠BAD=60°.
(1)连接AC,过点D作DE⊥AB于点E,DF⊥BC交AC于点F,DE、DF于点M、N.
①依题意补全图1;
②求MN的长;
(2)如图2,将(1)中∠EDF以点D为中心,顺时针旋转45°,其两边DE′、DF′分别与直线AB、BC相交于点Q、P,连接QP,请写出求△DPQ的面积的思路.(可以不写出计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系xOy中,A(3,4),B(1,2),C(5,1).

(1)作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元.
①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,
(1) 取点M(1,0),则点M到直线l: ![]() 的距离为_________,取直线
的距离为_________,取直线![]() 与直线l平行,则两直线距离为_________.
与直线l平行,则两直线距离为_________.
(2) 已知点P为抛物线y=x2-4x的x轴上方一点,且点P到直线l: ![]() 的距离为
的距离为![]() ,求点P的坐标.
,求点P的坐标.
(3) 若直线y=kx+m与抛物线y=x2-4x相交于x轴上方两点A、B(A在B的左边),且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离的最大时直线y=kx+m的解析式.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com