
【题目】如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.

(1)若当t的值为m时,PP′恰好经过点A,求m的值;
(2)设△P′PQ的面积为y,求y与t之间的函数关系式(m<t≤4) ;
(3)是否存在某一时刻t,使PQ平分角∠P′PC?存在,求相应的t值,不存在,请说明理由.
【答案】(1)m=![]() s;(2)y=78t2﹣504t+768(
s;(2)y=78t2﹣504t+768(![]() <t≤4);(3)存在,t=2时,PQ平分角∠P′PC .
<t≤4);(3)存在,t=2时,PQ平分角∠P′PC .
【解析】
试题(1)由∠C的余弦定义既在Rt△APC,又可在Rt△ACM中列出比例式,二者相等,构建方程,求出m;
(2)由△PCN∽△ACM,可表示出PC=40﹣10t,PN=P′N=24﹣6t,CN=32﹣8t,代入面积公式,即可得y=![]() PP′NQ=78t2﹣504t+768;
PP′NQ=78t2﹣504t+768;
(3)利用∠C的正弦有两种表示的比例式,二者相等,可列出方程,求出t.
试题解析:(1)如图1中,作AM⊥BC于M.
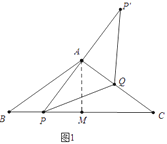
∵AB=AC=25,AM⊥BC,
∴BM=MC=20,
在Rt△ABM中,AM=![]() =15,
=15,
当PP′恰好经过点A,∵cos∠C=![]() ,
,
∴![]() ,
,
∴t= ![]() ,
,
∴m= ![]() s;
s;
(2)如图2中,设PP′交AC于N.

当 ![]() <t≤4时,由△PCN∽△ACM,可得PC=40﹣10t,PN=P′N=24﹣6t,CN=32﹣8t,
<t≤4时,由△PCN∽△ACM,可得PC=40﹣10t,PN=P′N=24﹣6t,CN=32﹣8t,
∵CQ=5t,
∴NQ=CN﹣CQ=32﹣13t,
∴y= ![]() PP′NQ=
PP′NQ= ![]() (48﹣12t)(32﹣13t)=78t2﹣504t+768(
(48﹣12t)(32﹣13t)=78t2﹣504t+768( ![]() <t≤4);
<t≤4);
(3)存在.理由如下:
如图3中,作QE⊥BC于E.

∵PQ平分∠CPP′,QE⊥PC,QN⊥PP′,
∴QN=QE,
∵sin∠C=![]() ,
,
∴![]()
∴t=2,
∴t=2时,PQ平分角∠P′PC.


科目:初中数学 来源: 题型:
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施.如图,京张高铁起自北京北站,途经清河、沙河、昌平等站,终点站为张家口南站,全长174千米.根据资料显示,京张高铁在某次测试中的平均时速是现运行的京张铁路某![]() 字头列车平均时速的6倍,全程行驶时间减少了122分钟,且每站(不计起始站和终点站)停靠的平均时间也减少了3.5分钟.请求出此次测试中京张高铁的平均时速是多少.
字头列车平均时速的6倍,全程行驶时间减少了122分钟,且每站(不计起始站和终点站)停靠的平均时间也减少了3.5分钟.请求出此次测试中京张高铁的平均时速是多少.
(注:平均时速的测算公式为![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图l、图2均为8×6的方格纸(每个小正方形的边长均为1),在方格纸中各有一条线段AB,其中点A、B均在小正方形的顶点上,请按要求画图:

(1)在图l中画一直角△ABC,使得tan∠BAC=![]() ,点C在小正方形的顶点上;
,点C在小正方形的顶点上;
(2)在图2中画一个□ABEF,使得□ABEF的面积为图1中△ABC面积的4倍,点E、F在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,△ACD、△CBE都是等边三角形,AE交DC于点M,BD交CE于点N,下列说法一定正确的是________(请把你认为正确答案的序号填在横线上)
①AE=BD;②∠AEC=∠BDC;③AM=DN;④DM=CN;⑤CM=MN;⑥MN∥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断中正确的有( )个
(1)直角三角形的两边为3和4,则第三边长为5
(2)有一个内角等于其它两个内角和的三角形是直角三角形
(3)若三角形的三边满足b2=a2﹣c2,则△ABC是直角三角形
(4)若△ABC中,∠A:∠B:∠C=8:15:17,则△ABC是直角三角形
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.

(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
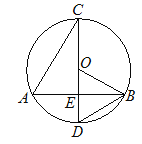
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com