
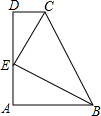
 如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )
如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )| CD |
| AD |
| DE |
| AE |
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
| A、2个 | B、3个 | C、4个 | D、5个 |
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
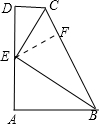 解:如图,过点E作EF⊥BC于点F;
解:如图,过点E作EF⊥BC于点F;| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |


科目:初中数学 来源: 题型:
| 1 |
| x |
| A、图象经过点(1,-1) |
| B、图象是中心对称图形 |
| C、图象位于第二、四象限 |
| D、当x<0时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、19×10-4千克 |
| B、1.9×10-6千克 |
| C、19×10-5千克 |
| D、1.9×10-5千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:
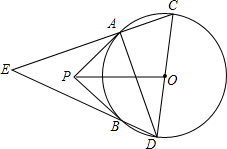 如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.
如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
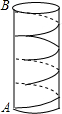 为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为
为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为查看答案和解析>>
科目:初中数学 来源: 题型:
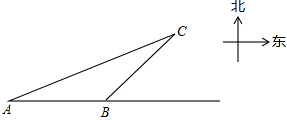 一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?
一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com