
【题目】如图,已知 ![]() 是
是 ![]() 的直径,过点
的直径,过点 ![]() 作弦
作弦 ![]() 的平行线,交过点
的平行线,交过点 ![]() 的切线
的切线 ![]() 于点
于点 ![]() ,连结
,连结 ![]() .
.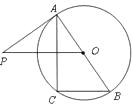
(1)求证: ![]() ;
;
(2)若 ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)证明:∵BC∥OP,
∴∠AOP=∠B,
∵AB是直径,
∴∠C=90°,
∵PA是⊙ O 的切线,切点为A,
∴∠OAP=90°,
∴∠C=∠OAP,
∴△ABC∽△POA
(2)解:∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
, ![]()
∴OA=2,AB=4
∴ ![]() ,
,
∴ ![]() ,
, ![]()
【解析】(1)根据已知BC∥OP,得出∠AOP=∠B,再根据AB是直径,PA是⊙ O 的切线,得出∠C=∠OAP,根据两组对应角相等的两三角形相似,即可证得结论。
(2)根据OB的长,就可求出AB的长,再根据△ABC∽△POA ,得出对应边成比例,即可求出BC的长。
【考点精析】利用圆周角定理和切线的性质定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】我国宋朝数学家杨辉在他的著作《详解九章算术》中提出下表,此表揭示了(n为非负整数)展开式的各项系数的规律,例如:
(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…
根据以上规律,(a+b)6展开式共有______项,各项系数的和等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
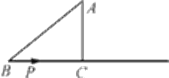
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).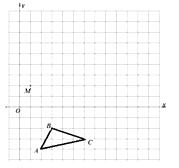
①画出△ABC关于 ![]() 轴对称的△A1B1C1;
轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2︰1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】x1、x2、x3、…x20是20个由1,0,﹣1组成的数,且满足:①x1+x2+x3+…+x20=4,②(x1﹣1)2+(x2﹣1)2+(x3﹣1)2…+(x20﹣1)2=32,则这列数中1的个数为_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ÷
÷![]() -
-![]() ×
×![]() +
+![]() ; (2)
; (2)![]() -
-![]() -(
-(![]()
![]() -2
-2![]() );
);
(3)(2-![]() )2017×(2+
)2017×(2+![]() )2016-2
)2016-2![]() -(-
-(-![]() )0 (4)(a+2
)0 (4)(a+2![]() +b)÷(
+b)÷(![]() +
+![]() )-(
)-(![]() -
-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)
①画出△ABC关于![]() x轴对称的△A1B1C1;
x轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com