

分析 (1)如图1,连接OD、AE、OE,根据已知条件得到AD,BC是⊙的切线,根据切线的性质得到CE=CB,∠OAD=$\frac{1}{2}$∠ABE,于是推出∠BEC=∠CBE,求得∠ODE=90°-∠DEA,根据圆周角定理得到∠AEB=90°,于是得到∠BEC=90°-∠DEA,等量代换得到∠ODE=∠BEC,即可得到结论.
(2)连接OE,根据切线的性质得到∠OED=90°,推出Rt△ADO≌Rt△ODE,根据全等三角形的性质得到∠AOD=∠EOD,同理∠EOC=∠BOC,于是得到∠DOC=∠DOE+∠COE=90°,根据勾股定理得到CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=10,由三角形的面积公式求得OE=$\frac{OD•OC}{CD}$=$\frac{24}{5}$,即可得到结论.
解答 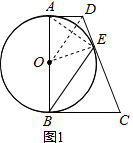 (1)证明:如图1,连接OD、AE、OE,
(1)证明:如图1,连接OD、AE、OE,
∵∠BAD=∠ABC=90°,
∴AD,BC是⊙的切线,
∵CD切⊙O于E,
∴CE=CB,∠OAD=$\frac{1}{2}$∠ABE,
∴∠BEC=∠CBE,
∵OA=OE,
∴OD⊥AE,
∴∠ODE=90°-∠DEA,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠BEC=90°-∠DEA,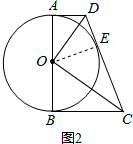
∴∠ODE=∠BEC,
∴∠ADC=2∠CBE;
(2)解:如图2,连接OE,
∵CD是⊙O的切线,
∴∠OED=90°,
在Rt△ADO与Rt△ODE中,$\left\{\begin{array}{l}{OA=OE}\\{OD=OD}\end{array}\right.$,
∴Rt△ADO≌Rt△ODE,
∴∠AOD=∠EOD,
同理∠EOC=∠BOC,
∴∠DOC=∠DOE+∠COE=90°,
∵OD=6,OC=8,
∴CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=10,
∴OE=$\frac{OD•OC}{CD}$=$\frac{24}{5}$,
∴⊙O的半径=$\frac{24}{5}$.
点评 本题主要考查切线的性质,全等三角形的判定和性质,利用切线长定理证明三角形全等得到角相等是解题的关键.


科目:初中数学 来源: 题型:选择题
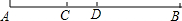 如图,已知线段AB=12cm,点C在线段AB上.且BC=2AC,D是线段AB的中点,则CD的长为( )
如图,已知线段AB=12cm,点C在线段AB上.且BC=2AC,D是线段AB的中点,则CD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
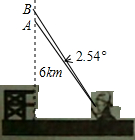 如图,一只运载火箭从地面L处发射,当卫星到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°,1s后,火箭到达B点,此时测得仰角为45.54°,这个火箭从A到B的平均速度是多少(精确到0.01km/s)?
如图,一只运载火箭从地面L处发射,当卫星到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°,1s后,火箭到达B点,此时测得仰角为45.54°,这个火箭从A到B的平均速度是多少(精确到0.01km/s)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
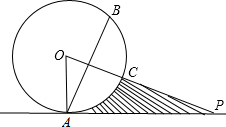 如图,点P在圆O外,PA与圆O相切于C点,点B与点A关于直线PO对称,已知OA=4,∠P=30°,求:
如图,点P在圆O外,PA与圆O相切于C点,点B与点A关于直线PO对称,已知OA=4,∠P=30°,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-3,2) | C. | (3,2) | D. | (2,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com