
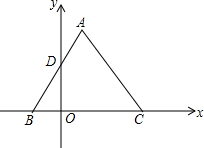
 如图是边长为4的等边△ABC,如果以BC所在直线为x轴,y轴经过AB的中点D点,请你求出点A、B、C的坐标.
如图是边长为4的等边△ABC,如果以BC所在直线为x轴,y轴经过AB的中点D点,请你求出点A、B、C的坐标. 分析 过A点作AM⊥x轴交x轴于点M,易得△BOD∽△BMA,由y轴经过AB的中点D点,利用等边三角形的性质易得点B的坐标,可得C点的坐标,由锐角三角函数可得A点坐标.
解答 解:过A点作AM⊥x轴交x轴于点M,
∵AM⊥x轴,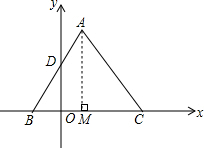
∴AM∥y轴,
易得△BOD∽△BMA,
∴$\frac{BO}{BM}=\frac{BD}{BA}=\frac{1}{2}$,
∴BM=2BO,
∵△ABC为边长为4等边三角形,
∴BM=2,
∴BO=1,
∴B(-1,0);
∵-1+4=3,
∴C(3,0);
∵AM=AB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴A(1,2$\sqrt{3}$),
∴点A、B、C的坐标分别为(1,2$\sqrt{3}$),(-1,0),(3,0).
点评 本题考查了等边三角形的性质及坐标与图形的知识,利用等边三角形的性质及锐角三角函数是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 利用一面长22米的墙围成一个形状为长方形的养鸡场.如图所示,养鸡场的一面靠墙其他三面用竹篱笆围成,并在一侧留有1米宽的门.现有长度为54米的竹篱笆.大李计划围成的养鸡场的长比宽多7米.小李计划围成的养鸡场的长比宽多4米,请你通过计算分析,谁的方案能够实现?此时养鸡场的面积是多少?
利用一面长22米的墙围成一个形状为长方形的养鸡场.如图所示,养鸡场的一面靠墙其他三面用竹篱笆围成,并在一侧留有1米宽的门.现有长度为54米的竹篱笆.大李计划围成的养鸡场的长比宽多7米.小李计划围成的养鸡场的长比宽多4米,请你通过计算分析,谁的方案能够实现?此时养鸡场的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
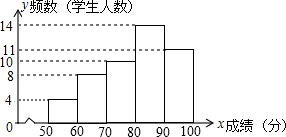 某班进行一次数学测试,根据测试成绩(得分为整数,满分为100分)绘制了频数分布图(如图所示,每组含最高分不含最低分),其中得分不超过50分的有3人,该班有5名学生的成绩为80分.根据所给信息解答下列问题:
某班进行一次数学测试,根据测试成绩(得分为整数,满分为100分)绘制了频数分布图(如图所示,每组含最高分不含最低分),其中得分不超过50分的有3人,该班有5名学生的成绩为80分.根据所给信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com