
【题目】某淘宝网店销售台灯,成本为每个30元,销售大数据分析表明,当每个台灯售价为40元时,平均每月售出600个,若售价每上涨1元,其月销量就减少20个,若售价每下降1元,其月销量就增加200个.
(1)若售价上涨![]() 元,每月能售出___________个台灯.
元,每月能售出___________个台灯.
(2)为迎接“双十一”,该网店决定降价销售,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
科目:初中数学 来源: 题型:
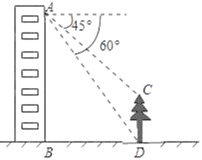
【题目】如图,小明在教学楼的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为10米.请你帮助小明计算树的高度(精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+m(k<0)与抛物线y=x2+bx+c相交于抛物线的顶点P和另一点Q.
(1)若点P(2,﹣c),Q的横坐标为﹣1.求点Q的坐标;
(2)过点Q作x轴的平行线与抛物线y=x2+bx+c的对称轴相交于点E,直线PQ与y轴交于点M,若PE=2EQ,c=![]() (﹣
(﹣![]() ≤b<﹣2),求点Q的纵坐标;
≤b<﹣2),求点Q的纵坐标;
(3)在(2)的条件下,求△OMQ的面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
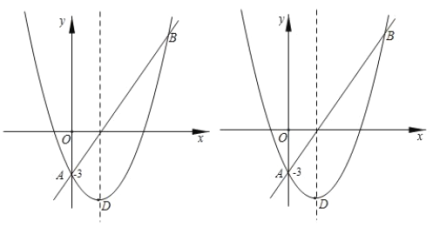
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价![]() 元,则平均每天销售数量为___________件(用含
元,则平均每天销售数量为___________件(用含![]() 的代数式表示);
的代数式表示);
(2)当每件商品降价多少元时,该商店每天销售利润为1050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
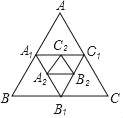
【题目】如图,已知等边三角形ABC边长为1,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成△A2B2C2,依此进行下去得到△A5B5C5的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有![]() 型产品
型产品![]() 件,
件,![]() 型产品
型产品![]() 件,分配给下属甲、乙两个商店销售,其中
件,分配给下属甲、乙两个商店销售,其中![]() 件给甲店,
件给甲店,![]() 件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
|
| |
甲店 |
|
|
乙店 |
|
|
(1)设分配给甲店![]() 型产品x件,则:
型产品x件,则:
①分配给乙店的![]() 型产品_________件;
型产品_________件;
②分配给乙店的![]() 型产品_________件.
型产品_________件.
(2)这家公司卖出这![]() 件产品的总利润为
件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(3)若公司要求总利润不低于![]() 元,说明有多少种不同分配方案,并将各种方案设计出来.
元,说明有多少种不同分配方案,并将各种方案设计出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com