
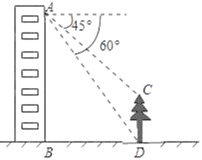
【题目】如图,小明在教学楼的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为10米.请你帮助小明计算树的高度(精确到0.1米).
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
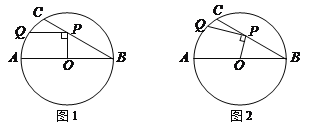
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程(按要求方法解方程,否则不得分,没有要求的请用适当的方法解方程)
(1)![]() (直接开方法) (2)
(直接开方法) (2)![]() (配方法)
(配方法)
(3)![]() (公式法) (4)
(公式法) (4)![]() (因式分解法)
(因式分解法)
(5)![]() (6)
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于半径为
中,对于半径为![]() 的
的![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称
,则称![]() 为
为![]() 的“近外点”.
的“近外点”.
(1)当![]() 的半径为2时,点
的半径为2时,点![]() ,
,![]() ,
,![]() ,
,![]() 中,
中,![]() 的“近外点”是__________;
的“近外点”是__________;
(2)若点![]() 是
是![]() 的“近外点”,求
的“近外点”,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)当![]() 的半径为2时,直线
的半径为2时,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若线段
,若线段![]() 上存在
上存在![]() 的“近外点”,直接写出
的“近外点”,直接写出![]() 的取值范围.
的取值范围.
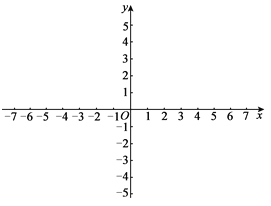
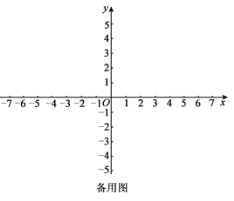
查看答案和解析>>
科目:初中数学 来源: 题型:
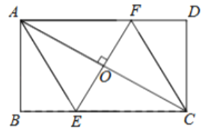
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=2,BC=4,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
已知,在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.

(1)(问题发现)
如图1,当∠EDF绕点D旋转到DE⊥AC于点E时(如图1),
①证明:△ADE≌△BDF;
②猜想:S△DEF+S△CEF= S△ABC.
(2)(类比探究)
如图2,当∠EDF绕点D旋转到DE与AC不垂直时,且点E在线段AC上,试判断S△DEF+S△CEF与S△ABC的关系,并给予证明.
(3)(拓展延伸)
如图3,当点E在线段AC的延长线上时,此时问题(2)中的结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?(写出你的猜想,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝网店销售台灯,成本为每个30元,销售大数据分析表明,当每个台灯售价为40元时,平均每月售出600个,若售价每上涨1元,其月销量就减少20个,若售价每下降1元,其月销量就增加200个.
(1)若售价上涨![]() 元,每月能售出___________个台灯.
元,每月能售出___________个台灯.
(2)为迎接“双十一”,该网店决定降价销售,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com