
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 旋转后能与
旋转后能与![]() 重合.
重合.

(1)旋转中心是哪一点?
(2)旋转角度是多少度?
(3)连结![]() 后,
后,![]() 是什么三角形?简单说明理由.
是什么三角形?简单说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
(1)证明:RP=RQ;
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.

B、变化二:运动探求. ①如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断) 答:_________.
②如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,如图1,若∠BCA=90°,∠α=90°,则BE______CF;并说明理由.
(2)如图2,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想:__________.并说明理由.
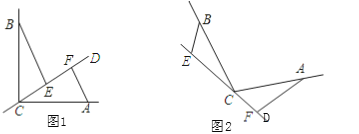
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
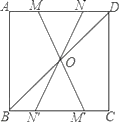
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com