
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值: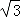 =1.732,
=1.732, =1.414)
=1.414)

【考点】解直角三角形的应用-仰角俯角问题.
【分析】设CF=x,在Rt△ACF和Rt△BCF中,分别用CF表示AC、BC的长度,然后根据AC﹣BC=1200,求得x的值,用h﹣x即可求得最高海拔.
【解答】解:设CF=x,
在Rt△ACF和Rt△BCF中,
∵∠BAF=30°,∠CBF=45°,
∴BC=CF=x,
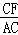 =tan30°,
=tan30°,
即AC= x,
x,
∵AC﹣BC=1200米,
∴ x﹣x=1200,
x﹣x=1200,
解得:x=600(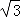 +1),
+1),
则DF=h﹣x=2001﹣600(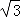 +1)≈362(米).
+1)≈362(米).
答:钓鱼岛的最高海拔高度约362米.
【点评】本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形求出AC、BC的长度,难度一般.


科目:初中数学 来源: 题型:
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
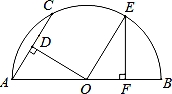
A.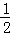 B.
B.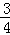 C.1 D.2
C.1 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
一元二次方程x2﹣2(3x﹣2)+(x+1)=0的一般形式是( )
A.x2﹣5x+5=0 B.x2+5x﹣5=0 C.x2+5x+5=0 D.x2+5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
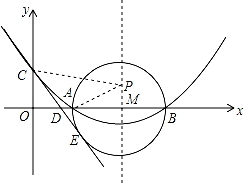
如图,已知抛物线的对称轴为直线l:x=4,且与x轴交于点A(2,0),与y轴交于点C(0,2).
(1)求抛物线的解析式;
(2)试探究在此抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径作⊙M,过点C作直线CE与⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com