
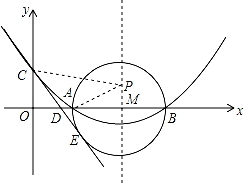
如图,已知抛物线的对称轴为直线l:x=4,且与x轴交于点A(2,0),与y轴交于点C(0,2).
(1)求抛物线的解析式;
(2)试探究在此抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径作⊙M,过点C作直线CE与⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
【考点】二次函数综合题.
【分析】(1)利用顶点式,根据待定系数法即可求得二次函数的解析式;
(2)线段BC的长即为AP+CP的最小值;
(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x, 在RT△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可.
在RT△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可.
【解答】解:(1)如图1,由题意,设抛物线的解析式为:y=a(x﹣4)2+k(a≠0)
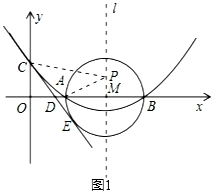
∵抛物线经过A(2,0)、C(0,2).
∴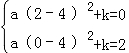 ,
,
解得:a=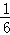 ,
,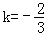 .
.
∴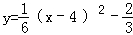 ,
,
即: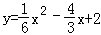 .
.
令y=0,得x2﹣8x+12=0,
即(x﹣2)(x﹣6)=0,
∴x1=2,x2=6.
∴抛物线与x轴另﹣交于点B(6,0).
(2)存在.
如本题图2,连接CB交l于点P,则点P即是使AP+CP的值最小的点.
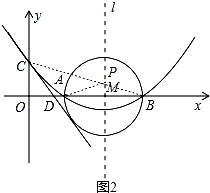
∵A、B关于l对称,
∴AP=BP,
∴AP+CP=CB,即AP+CP的最小值为BC.
∵OB=6,OC=2,
∴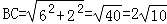 .
.
∴AP+CP的最小值为 ;
;
(3)如图3,连接ME,
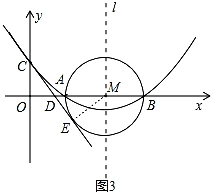
∵CE是⊙M的切线,
∴ME⊥CE,∠CEM=90°,
由题意,得OC=ME=2,∠ODC=∠MDE.
在△COD与△MED中,
 ,
,
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM,
设OD=x,则CD=DM=OM﹣OD=4﹣x,
则在Rt△C OD中,
OD中,
又 ∵OD2+OC2=CD2,
∵OD2+OC2=CD2,
∴x2+22=(4﹣x)2,
解得 ,
,
∴D(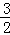 ,0),
,0),
设直线CE的解析式为y=mx+b,
∵直线CE过C(0,2)、D(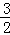 ,0)两点,
,0)两点,
∴ ,
,
解方程组得: .
.
∴直线CE的解析式为y=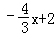 .
.
【点评】本题考查了二次函数的综合知识以及利用轴对称求最短路径和待定系数法求一次函数和二次函数解析式等知识,利用数形结合得出D点坐标是解题关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
运动会上,初二(3)班啦啦队,买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为x元,根据题意可列方程为( )
A.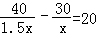 B.
B.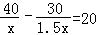
C.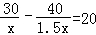 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值: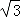 =1.732,
=1.732, =1.414)
=1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在正方形ABCD中,E是BC边的中点,把△ABE沿直线AE折叠,点B的对应点为B′,AB′的延长线交DC于点F,若FC=2,则正方形的边长为 .


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com