练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC中，AE交BC于点D，∠C=∠E，AD：DE=3：5，AE=8，BD=4，求DC的长．

    　


    【考点】相似三角形的判定与性质．

    【分析】根据相似三角形的判定与性质，可得=，再根据AD：DE=3：5，AE=8，可得AD、DE的长，根据比例的性质，可得答案．

    【解答】解：∵∠C=∠E，∠ADC=∠BDE，

    ∴△ADC∽△BDE，

    ∴=，

    又∵AD：DE=3：5，AE=8，

    ∴AD=3，DE=5，

    ∵BD=4，

    ∴=，即．

    ∴DC=．

    【点评】本题考查了相似三角形的判定与性质，利用了相似三角形的判定与性质，比例的性质．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知xm=6，xn=3，则的x2m﹣n值为(     )

    A．9       B．      C．12     D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A（﹣2，4），B（1，1），则关于x的方程ax2﹣bx﹣c=0的解为　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别，随机从口袋中任取一只球，取得黄球的可能性的大小是（　　）

    A．    B．    C．    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知y与x﹣1成反比例，且当x=3时，y=2，则y关于x的函数关系式为　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


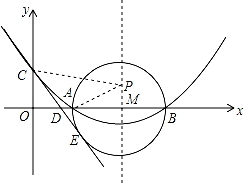
    如图，已知抛物线的对称轴为直线l：x=4，且与x轴交于点A（2，0），与y轴交于点C（0，2）．

    （1）求抛物线的解析式；

    （2）试探究在此抛物线的对称轴l上是否存在一点P，使AP+CP的值最小？若存在，求AP+CP的最小值，若不存在，请说明理由；

    （3）以AB为直径作⊙M，过点C作直线CE与⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    对于反比例函数y=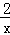，下列说法不正确的是(     )

    A．点（﹣2，﹣1）在它的图象上     B．它的图象在第一、三象限

    C．当x＞0时，y随x的增大而增大 D．当x＜0时，y随x的增大而减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    四张扑克牌的牌面如图1所示，将扑克牌洗匀后，如图2背面朝上放置在桌面上，小明和小亮设计了A、B两种游戏方案：

    方案A：随机抽一张扑克牌，牌面数字为5时小明获胜；否则小亮获胜．

    方案B：随机同时抽取两张扑克牌，两张牌面数字之和为偶数时，小明获胜；否则小亮获胜．

    请你帮小亮选择其中一种方案，使他获胜的可能性较大，并说明理由．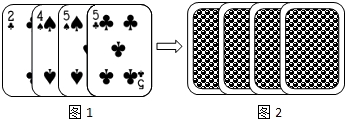

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若x=﹣2是关x于的方程x2﹣4mx﹣8=0的一个解，则m的值为　　　　　　．

    查看答案和解析>>

    同步练习册答案