
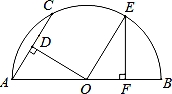
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
A.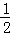 B.
B.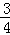 C.1 D.2
C.1 D.2
C【考点】垂径定理;全等三角形的判定与性质.
【分析】根据垂径定理求出AD,证△ADO≌△OFE,推出OF=AD,即可求出答案.
【解答】解:∵OD⊥AC,AC=2,
∴AD=CD=1,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵OE∥AC,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EF=90°,
∴∠DAO=∠EOF,
在△ADO和△OFE中,
 ,
,
∴△ADO≌△OFE(AAS),
∴OF=AD=1,
故选C.
【点评】本题考查了全等三角形的性质和判定,垂径定理的应用,解此题的关键是求出△ADO≌△OFE和求出AD的长,注意:垂直于弦的直径平分这条弦.


科目:初中数学 来源: 题型:
运动会上,初二(3)班啦啦队,买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为x元,根据题意可列方程为( )
A.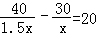 B.
B.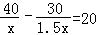
C.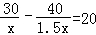 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线y=x2向左平移1个单位,再向下平移2个单位,得到新的图象的二次函数表达式是( )
A.y=(x+1)2+2 B.y=(x﹣1)2﹣2 C.y=(x+1)2﹣2 D.y=(x﹣1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值: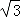 =1.732,
=1.732, =1.414)
=1.414)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com