
| m |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
|
| 1+k2 |
| m |
| x |
| m |
| 1 |
| 2 |
| x |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
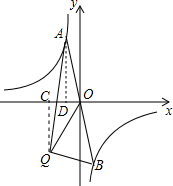
| CQ2+OC2 |
|
| AD2+OD2 |
| 1+k2 |
|
| 1+k2 |
2
| ||
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 品种 | 水稻 | 蔬菜 | 柑桔 |
| 亩产(公斤/亩) | 500 | 1000 | 200(只部分树木挂果) |
| 面积(亩) | 150 | 100 | 50 |
| 平均销售价(元/公斤) | 1.20 | 1.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:
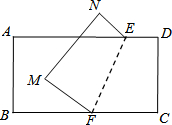 如图,将一张长方形的纸片沿折痕E、F翻折,使点C、D分别落在点M、N的位置,且∠BFM=
如图,将一张长方形的纸片沿折痕E、F翻折,使点C、D分别落在点M、N的位置,且∠BFM=| 1 |
| 2 |
| A、30° | B、36° |
| C、45° | D、60° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、x1+x2=1,x1•x2=-2 |
| B、x1+x2=-1,x1•x2=2 |
| C、x1+x2=1,x1•x2=2 |
| D、x1+x2=-1,x1•x2=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
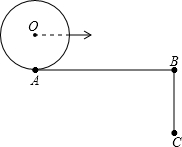 如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动点C时停止,则在此运动过程中,圆心O运动的总路程为
如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动点C时停止,则在此运动过程中,圆心O运动的总路程为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com