
 如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.| BC2-BD2 |
| 152-92 |
| AC2-CD2 |
| 202-122 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
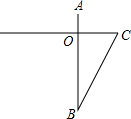 八年级学生准备测量校园人工湖的深度,他们把一根竹竿垂直插到离湖边1米的水底,只见竹竿高出水面1尺,把竹竿的顶端拉向湖边(底端不变),竿顶和湖沿的水面刚好平齐,求湖水的深度和竹竿的长.
八年级学生准备测量校园人工湖的深度,他们把一根竹竿垂直插到离湖边1米的水底,只见竹竿高出水面1尺,把竹竿的顶端拉向湖边(底端不变),竿顶和湖沿的水面刚好平齐,求湖水的深度和竹竿的长.查看答案和解析>>
科目:初中数学 来源: 题型:
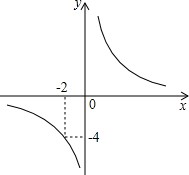 八(1)班课外学习小组对不等式
八(1)班课外学习小组对不等式 | 8 |
| x |
| 8 |
| x |
| 8 |
| x |
| 8 |
| x |
| 8 |
| x |
| 8 |
| x |
| 8 |
| x |
| 2 |
| x |
| -2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 项目 | 第一年的工资(万元) | 一年后的计算方法 |
| 基础工资 | 2 | 每年的增长率相同 |
| 工龄工资 | 0.08 | 每年增加0.08万元 |
| 岗位工资 | 0.2768 | 固定不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 1 |
| (x-1)(x+1) |
| 1 |
| (x+1)(x+3) |
| 1 |
| (x+3)(x+5) |
| 1 |
| (x+5)(x+7) |
| 1 |
| (x+7)(x+9) |
| 1 |
| (x+9)(x+11) |
查看答案和解析>>
科目:初中数学 来源: 题型:
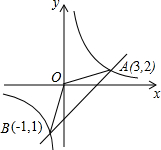 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com