
【题目】一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数,将骰子抛掷两次,将掷第一次后朝上一面的点数记为x,掷第二次后朝上一面的点数记为y.
(1)求点(x,y)在直线y=2x上的概率;
(2)求点(x,y)在直线y=-2x+7上的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】列表列举出所有情况;
(1)根据列表看落在直线y=2x上的情况占总情况的多少即可;
(2)根据列表看落在直线y=-2x+7上的情况占总情况的多少即可.
y x | 1 | 2 | 3 | 4 | 5 | 6 |
1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
(1)由列表法可以得出点(x,y)共有36种等可能的结果,
其中点(1,2),(2,4),(3,6)在直线y=2x上,
∴点(x,y)在直线y=2x上的概率是![]() ;
;
(2)根据题意,得1≤-2x+7≤6,解得![]() ≤x≤3.
≤x≤3.
∵x为整数,∴x为1,2,3,
要使点(x,y)在直线y=-2x+7上,
则对应的y值为5,3,1,
∴满足条件的点(x,y)有(1,5),(2,3),(3,1),
由列表可知点(x,y)共有36种等可能结果,
∴点(x,y)在直线y=-2x+7上的概率是![]() .
.


科目:初中数学 来源: 题型:
【题目】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.

(第22题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮参加中华诗词大赛,还剩最后两题,如果都答对,就可顺利通关.其中第一道单选题有4个选项,第二道单选题有3个选项.小亮这两道题都不会,不过还有一个“求助”没有使用(使用求助可以让主持人去掉其中一题的一个错误选项).
(1)如果小亮第一题使用“求助”,那么他答对第一道题的概率是__;
(2)他的亲友团建议:最后一题使用“求助”,从提高通关的可能性的角度看,你同意亲友团的观点吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
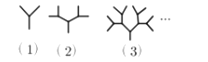
【题目】如图是由一些长度相等的小木棍组成的图形,图(1)(2)(3)需要的小木棍数量分别为3根、7根、15根,按照这种方式摆下去,第(4)个图形需要的木棍数量为__________,第(6)个图形需要的木棍数量为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一口袋中装有四根长度分别为1 cm,3 cm,4 cm,5 cm的细木棒,小明手中有一根长度为3 cm的细木棒,现随机从口袋中取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:
(1)求这三根细木棒能构成三角形的概率;
(2)求这三根细木棒能构成直角三角形的概率;
(3)求这三根细木棒能构成等腰三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修站,甲小组乘坐一辆汽车,沿东西方向的公路进行检修线路,约定向东为正,从![]() 地出发到收工时,行走记录为(单位:
地出发到收工时,行走记录为(单位:![]() ): +8,- 2, -13, -1, +10.同时,乙小组也从
): +8,- 2, -13, -1, +10.同时,乙小组也从![]() 地出发, 沿南北方向的公路检修线路,约定向北为正,行走记录为: -7, +9,- 2, +8,- 6.
地出发, 沿南北方向的公路检修线路,约定向北为正,行走记录为: -7, +9,- 2, +8,- 6.
(1)分别计算收工时,甲,乙两组各在![]() 地的哪一边,分别距离
地的哪一边,分别距离![]() 地多远?
地多远?
(2)若每千米汽车汽油消耗为0.3![]() ,求出发到收工时两组各耗油多少升?
,求出发到收工时两组各耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
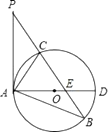
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=12,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com