
 如图所示:点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+2|+|b-6|=0.
如图所示:点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+2|+|b-6|=0.分析 (1)利用非负数的性质得出a、b的数值即可;
(2)设运动t秒时,两点相遇,根据行驶的路程和为AB之间的距离列出方程求得t,再利用移动规律求得相遇时数轴上的点表示的数;
(3)设经过a秒点B追上点A,根据行驶的路程差为AB之间的距离列出方程求得a,进一步利用速度×时间得出一共行驶了多少个单位长度即可.
解答 解:(1)∵|a+2|+|b-6|=0
∴a=-2,b=6,
点A表示的数是-2,点B表示的数是6,线段AB的长度是8.
(2)设运动t秒时,两点相遇,由题意得
t+3t=8
解得:t=2,
相遇时数轴上的点表示的数-1+1×2=1;
(2)设经过a秒点B追上点A,由题意得
3a-a=8
解得:a=4,
则4×2=8.
答:一共行驶了8个单位长度.
点评 此题考查一元一次方程的实际运用,结合数轴,掌握行程问题中的基本数量关系是解决问题的关键.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
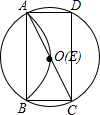 已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE.
已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{10}$×$\frac{8}{5}$=1 | B. | $\frac{4}{5}$÷5=4 | C. | (4$+\frac{1}{2}$)×$\frac{3}{4}$=4×$\frac{3}{4}$$+\frac{1}{2}$ | D. | $\frac{2}{3}$÷2=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
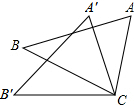 如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com