
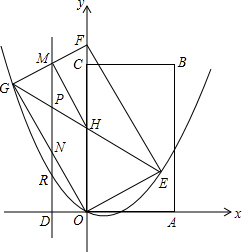
 ��ͼ������OABC�Ķ���A��2��0����C��0��2$\sqrt{3}$����������OABC�Ƶ�O��ʱ����ת30�㣬�þ���OEFG���߶�GE��FO�ཻ�ڵ�H��ƽ����y���ֱ��MN�ֱ��߶�FG��GH��GO��x���ڵ�M��P��N��D������MH
��ͼ������OABC�Ķ���A��2��0����C��0��2$\sqrt{3}$����������OABC�Ƶ�O��ʱ����ת30�㣬�þ���OEFG���߶�GE��FO�ཻ�ڵ�H��ƽ����y���ֱ��MN�ֱ��߶�FG��GH��GO��x���ڵ�M��P��N��D������MH���� ��1�������ʽһ����ô���ϵ������ͨ�������ϵĵ����㷽�������
��2��ƽ���ı��ζԱ�ƽ������ȣ�ǡ��MNΪ$\frac{1}{2}$OF����Ϊ��λ�ߣ������������ã�DΪx���ϵĵ㣬����������Ϊ0��
��3����֪S��Χ�������ķ�Χ����ô��ʾS�ǹؼ�����PH��Ϊƽ����x���y����߶Σ����Կ������ù������ƽ����y���ֱ����������Ϊ2�������εij��淽�������⣬�˷���Ϊ����������ò��Ϊ������IJ�����ɱ�ʾ��S����Ҫע�⣬��Q��O���ұ�ʱ������������Ϊ�������εIJ�ù�ϵʽ�ٴ���$\frac{\sqrt{3}}{6}$$��s��\frac{\sqrt{3}}{2}$����ⲻ��ʽ���ɣ���Ҫע�����������Ҫ����Q������R��E֮������ƣ�
��� 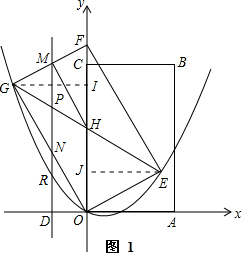 �⣺��1����ͼ1����G��GI��CO��I����E��EJ��CO��J��
�⣺��1����ͼ1����G��GI��CO��I����E��EJ��CO��J��
��A��2��0����C��0��2$\sqrt{3}$����
��OE=OA=2��OG=OC=2$\sqrt{3}$��
�ߡ�GOI=30�㣬��JOE=90��-��GOI=90��-30��=60�㣬
��GI=sin30��•GO=$\frac{1}{2}$•2$\sqrt{3}$=$\sqrt{3}$��
IO=cos30��•GO=$\frac{\sqrt{3}}{2}$•2$\sqrt{3}$=3��
JE=cos30��•OE=$\frac{\sqrt{3}}{2}$•2=$\sqrt{3}$��
JO=sin30��•OE=$\frac{1}{2}$•2=1��
��G��-$\sqrt{3}$��3����E��$\sqrt{3}$��1����
�������߽���ʽΪy=ax2+bx+c��
�߾���G��O��E���㣬
��$\left\{\begin{array}{l}{3a-\sqrt{3}b+c=3}\\{3a+\sqrt{3}b+c=1}\\{0+0+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-\frac{\sqrt{3}}{3}}\\{c=0}\end{array}\right.$��
��y=$\frac{2}{3}$x2-$\frac{\sqrt{3}}{3}$x��
��2�������ı���OHMNΪƽ���ı��Σ�
��MN��OH��MN=OH��
��OH=$\frac{1}{2}$OF��
��MNΪ��OGF����λ�ߣ�
��xD=xN=$\frac{1}{2}$•xG=-$\frac{\sqrt{3}}{2}$��
��D��-$\frac{\sqrt{3}}{2}$��0����
��3����ֱ��GE�Ľ���ʽΪy=kx+b��
��G��-$\sqrt{3}$��3����E��$\sqrt{3}$��1����
��$\left\{\begin{array}{l}{-\sqrt{3}k+b=3}\\{\sqrt{3}k+b=1}\end{array}\right.$��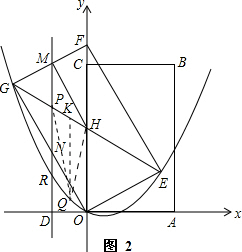
��ã�$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2}\end{array}\right.$��
��y=-$\frac{\sqrt{3}}{3}$x+2��
��Q��������y=$\frac{2}{3}$x2-$\frac{\sqrt{3}}{3}$x�ϣ�
����Q��������x��$\frac{2}{3}$x2-$\frac{\sqrt{3}}{3}$x����
��Q��R��E����֮���˶���
��-$\frac{\sqrt{3}}{2}$��x��$\sqrt{3}$��
�ٵ�-$\frac{\sqrt{3}}{2}$��x��0ʱ��
��ͼ2������PQ��HQ������Q��QK��y�ᣬ��GE��K����K��x��-$\frac{\sqrt{3}}{3}$x+2����
��S��PKQ=$\frac{1}{2}$•��yK-yQ��•��xQ-xP����
S��HKQ=$\frac{1}{2}$•��yK-yQ��•��xH-xQ����
��S��PQH=S��PKQ+S��HKQ=$\frac{1}{2}$•��yK-yQ��•��xQ-xP��+$\frac{1}{2}$•��yK-yQ��•��xH-xQ��
=$\frac{1}{2}$•��yK-yQ��•��xH-xP��=$\frac{1}{2}$•[-$\frac{\sqrt{3}}{3}$x+2-��$\frac{2}{3}$x2-$\frac{\sqrt{3}}{3}$x��]•[0-��-$\frac{\sqrt{3}}{2}$��]=-$\frac{\sqrt{3}}{6}$x2+$\frac{\sqrt{3}}{2}$��
�ڵ�0��x��$\sqrt{3}$ʱ��
��ͼ3������PQ��HQ������Q��QK��y�ᣬ��GE��K����K��x��-$\frac{\sqrt{3}}{3}$x+2����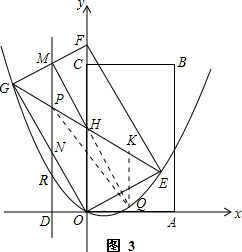
ͬ�� S��PQH=S��PKQ-S��HKQ=$\frac{1}{2}$•��yK-yQ��•��xQ-xP��-$\frac{1}{2}$•��yK-yQ��•��xQ-xH��
=$\frac{1}{2}$•��yK-yQ��•��xH-xP��
=-$\frac{\sqrt{3}}{6}$x2+$\frac{\sqrt{3}}{2}$��
����������S��PQH=-$\frac{\sqrt{3}}{6}$x2+$\frac{\sqrt{3}}{2}$��
��$\frac{\sqrt{3}}{6}$��s��$\frac{\sqrt{3}}{2}$��
��$\frac{\sqrt{3}}{6}$��-$\frac{\sqrt{3}}{6}$x2+$\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}$��
��ã�-$\sqrt{2}$��x��$\sqrt{2}$��
��-$\frac{\sqrt{3}}{2}$��x��$\sqrt{3}$��x��0��
��-$\frac{\sqrt{3}}{2}$��x��$\sqrt{2}$��x��0��
���� ���⿼����һ�κ��������κ���������ͼ��ֱ�������μ�����ϵ������������ı�ʾ��֪ʶ�㣮ע�����С����ù������ƽ����y���ֱ����������Ϊ2�������εij��淽������ʾ������ǽ������п��Ŀ����ȵ㣬��Ҫ��ǿ�������ã�


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
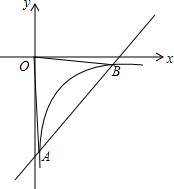 ��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ཻ�ڵ�A��1��-4������B��3��n����
��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ཻ�ڵ�A��1��-4������B��3��n�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a2=a4 | B�� | ��a3��3=a9 | C�� | ��a+1��2=a2+1 | D�� | 1+$\frac{1}{a}=\frac{2}{a}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
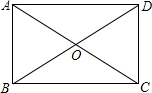 ��ͼ����֪�����ı���ABCD�У�AO=BO=CO=DO����֤���ı���ABCD�Ǿ��Σ�
��ͼ����֪�����ı���ABCD�У�AO=BO=CO=DO����֤���ı���ABCD�Ǿ��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{16}$ | B�� | 3.14 | C�� | $\frac{3}{11}$ | D�� | -�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com