
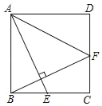
【题目】如图,在正方形ABCD中,点E是BC上一点,BF⊥AE交DC于点F,若AB=5,BE=2,则AF=____.
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
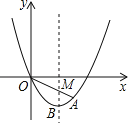
【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a≠0)经过点A(6,﹣3),对称轴是直线x=4,顶点为B,OA与其对称轴交于点M,M、N关于点B对称.
(1)求这条抛物线的表达式和点B的坐标;
(2)联结ON、AN,求△OAN的面积;
(3)点Q在x轴上,且在直线x=4右侧,当∠ANQ=45°时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为“创建文明城市,构建和谐社会”.更好的提高业主垃圾分类的意识,业主委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱.若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.
(1)问:购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共10个,费用不超过800元,问:最多购买垃圾箱多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
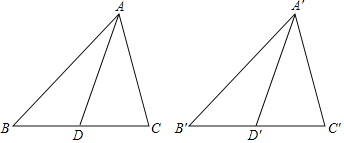
【题目】已知,如图,在△ABC和△A'B'C'中,AD,A'D'分别是△ABC和△A'B'C'的中线,AB=A'B',BC=B'C',AD=A'D'.求证:△ABC≌△A'B'C'.
查看答案和解析>>
科目:初中数学 来源: 题型:
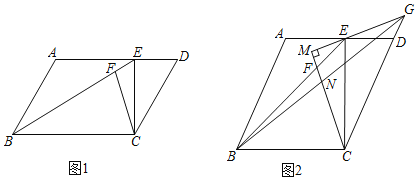
【题目】如图,在平行四边形ABCD中,CE⊥BC交AD于点E,连接BE,点F是BE上一点,连接CF.
(1)如图1,若∠ECD=30°,BC=4,DC=2,求tan∠CBE的值;
(2)如图2,若BC=EC,过点E作EM⊥CF,交CF延长线于点M,延长ME、CD相交于点G,连接BG交CM于点N且CM=MG,
①在射线GM上是否存在一点P,使得△BCP≌△ECG?若存在,请指出点P的位置并证明这对全等三角形;若没有,请说明理由.
②求证:EG=2MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).
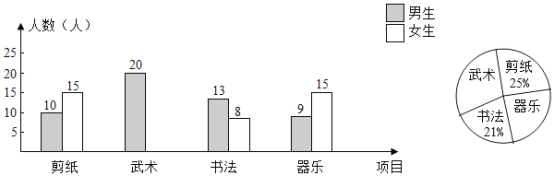
请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,
①用尺规作出点A到CD所在直线的距离;
②求出该距离.
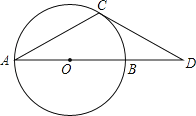
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com