
����Ŀ��Ϊ��ǿѧ�����������ʣ������������Ź涨ѧ��ÿ��μӻ�����ƽ��ʱ�䲻����1Сʱ��Ϊ�˽�ѧ���μӻ�����������Բ���ѧ���μӻ�����ʱ������˳������飬�������������Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
(1)����ε����й������˶�����ѧ����
(2)����ʱ��Ϊ1.5Сʱ������������ȫƵ���ֲ�ֱ��ͼ��
(3)���ε�����ѧ���μӻ�����ƽ��ʱ���Ƿ����Ҫ��
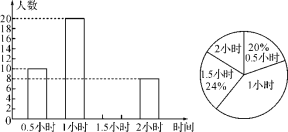
���𰸡���1��50������2��12�ˣ�������������3�����ε�����ѧ���μӻ�����ƽ��ʱ�����Ҫ��
��������
���⣨1����������=10��20%=50���ˣ�
1.5Сʱ�������ǣ�50��24%=12���ˣ���
��2����ʾ����ʱ��1Сʱ������Բ�ĽǵĶ���=![]() ��360��=144����
��360��=144����
��3��������ƽ��ʱ��=![]() =1.18��Сʱ����
=1.18��Сʱ����
��1.18��1
��ƽ���ʱ������ϼ�Ҫ����ʱ�����������λ����Ϊ1���������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2010��5��1�գ���41�����������Ϻ��ٰ죬����֪ʶ��УѸ�ٴ�����С��ͬѧ�ͱ���ѧ��������֪ʶ���˽�̶Ƚ�����һ�ε���ͳ�ƣ���ͼ�����ɼ����ݺ���Ƶ�������������ͳ��ͼ��A�����˽⣬B��һ���˽⣬C���˽�϶࣬D����Ϥ�����������ͼ���ṩ����Ϣ����������⣺

��1����ð�ж�����ѧ����
��2��������ͳ��ͼ�У�����ʾ��һ���˽����IJ��ֲ���������
��3��������ͳ��ͼ�У���������˽�϶�����������Ӧ��Բ�ĽǵĶ�����
��4���Ӹð�����ѡһ�ˣ��������֪ʶ���˽�̶�Ϊ����Ϥ���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0���������㣨1.0�����Գ���l��ͼ��ʾ����M��a+b��c��N��2a��b��P��a+c����M��N��P�У�ֵС��0�����У�����������
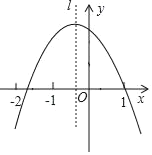
A.2B.1C.0D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�İ뾶Ϊ5����ABC�ǡ�O���ڽ������Σ�AB��8��������B����O������BD������A��AD��BD������ΪD��
��1����֤����BAD+��C��90��
��2�����߶�AD�ij���
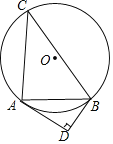
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A��B��C������ֱ�Ϊ��0��5����0��2����4��2����ֱ��l�Ľ���ʽΪy = kx+5��4k��k > 0����
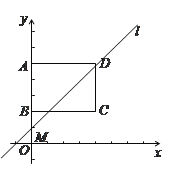
��1����ֱ��l������Bʱ����һ�κ����Ľ���ʽ��
��2��ͨ������˵��������kΪ��ֵ��ֱ��l�ܾ�����D��
��3��ֱ��l��y�ύ�ڵ�M����N���߶�DM�ϵ�һ�㣬 ����NBDΪ���������Σ���̽����
��������y = kx+5��4kΪ����������ʱ����N�ĸ����� ����
����M�ڲ�ͬλ��ʱ��k��ȡֵ����Ӧ�仯����N�ĸ���������ܻ�ı䣬��ֱ��д����N���в�ͬ�ĸ�������Լ���Ӧ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��8��BC��4����������AC�۵�����D���ڵ�D���������ص����֡�AFC�����Ϊ�� ��

A.6B.8C.10D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ������a��0��
������a��0��
��1��������![]() ������ʵ��
������ʵ��![]() ���ҷ���
���ҷ���![]() ��������ȵ�ʵ��������κ����Ľ���ʽ��
��������ȵ�ʵ��������κ����Ľ���ʽ��
��2�������κ���![]() ��ͼ����x�ύ��
��ͼ����x�ύ��![]() ���㣬�ҵ�
���㣬�ҵ�![]() ʱ��
ʱ��![]() ���������ʵ��m��ȡֵ��Χ��
���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶ѧ��������ʵ������������������40��ͬѧʵ������ĵ÷֣����ݻ�ȡ���������ݣ����������µ�����ͳ��ͼ������ͳ��ͼ������������Ϣ������������⣺
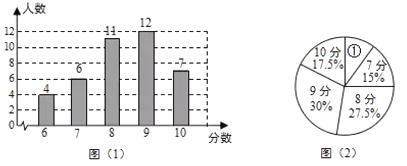
��1�����е�����ӦΪ��6��![]() ��������
��������![]() ��ֵΪ �����ٵ�Բ�ĽǵĴ�С�� ��
��ֵΪ �����ٵ�Բ�ĽǵĴ�С�� ��
��2������40���������ݵ�ƽ��������������λ����
��3������У���꼶����360��ѧ�������Ƹ�У����ʵ����������ֵ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com