
ΓΨΧβΡΩΓΩ»ΞΡξ3‘¬Θ§Ρ≥≥¥ΖΩΆ≈“‘≤ΜΕύ”Ύ2224Άρ‘Σ≤Μ…Ό”Ύ2152Άρ‘ΣΒΡΉ ΫπΖ÷±π¥”A≥«ΓΔB≥«¬ρ»κ–ΓΜß–ΆΕΰ ÷ΖΩΘ®80ΤΫΖΫΟΉ/ΧΉΘ©Ι≤4000ΤΫΖΫΟΉ.Τδ÷–A≥«ΓΔB≥«ΒΡΙΚ»κΦέΗώΖ÷±πΈΣ4000‘Σ/ΤΫΖΫΟΉΓΔ7000‘Σ/ΤΫΖΫΟΉ.Ή‘ΉΓΫ®≤ΩΫώΡξ5‘¬‘ΦΧΗ≥…ΕΦ –’ΰΗ°ΗΚ‘πΆ§÷ΨΚσΘ§≥…ΕΦ –Ϋχ“Μ≤ΫΦ”¥σΝΥΒςΩΊ’ΰ≤Ώ.Ρ≥≥¥ΖΩΆ≈ΈΣ≈Ή έA≥«ΒΡΕΰ ÷ΖΩΘ§ΨωΕ®¥”6‘¬ΤπΟΩΤΫΖΫΟΉΫΒΦέ1000‘Σ.»γΙϊ¬τ≥ωœύΆ§ΤΫΖΫΟΉΒΡΖΩΉ”Θ§Ρ«Ο¥5‘¬ΒΡœζ έΕνΈΣ640Άρ‘ΣΘ§6‘¬ΒΡœζ έΕνΈΣ560Άρ‘Σ.
Θ®1Θ©A≥«ΫώΡξ6‘¬ΟΩΤΫΖΫΟΉΒΡ έΦέΈΣΕύ…Ό‘ΣΘΩ
Θ®2Θ©«κΈ »ΞΡξ3‘¬”–ΦΗ÷÷ΙΚ»κΖΫΑΗΘΩ
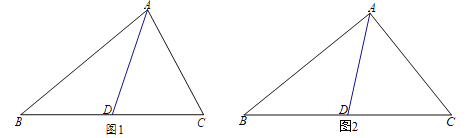
Θ®3Θ©»τ»ΞΡξ»ΐ‘¬ΥυΙΚΖΩ≤ζ»Ϊ≤ΩΟΜ”–¬τ≥ωΘ§≥¥ΖΩΆ≈ΦΤΜ°‘Ύ7‘¬÷¥––œζ έΖΫΑΗΘΚB≥« έΦέΈΣ1.05Άρ‘Σ/ΤΫΖΫΟΉΘ§≤Δ«“ΟΩ έ≥ω“ΜΧΉΖΒΜΙΗΟΙΚΖΩ’Ώa‘ΣΘΜA≥«Α¥ΫώΡξ6‘¬ΒΡΦέΗώΫχ––œζ έΓΘ“Σ ΙΘ®2Θ©÷–ΒΡΥυ”–ΖΫΑΗάϊ»σœύΆ§Θ§«σ≥ωa”Π»ΓΚΈ÷ΒΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©A≥«ΫώΡξ6‘¬ΟΩΤΫΖΫΟΉΒΡ έΦέΈΣ![]() ‘ΣΘΜΘ®2Θ©ΖΫΑΗ”–ΥΡ÷÷Θ§»γ±μΥυ ΨΦϊΫβΈωΘΜΘ®3Θ©
‘ΣΘΜΘ®2Θ©ΖΫΑΗ”–ΥΡ÷÷Θ§»γ±μΥυ ΨΦϊΫβΈωΘΜΘ®3Θ©![]() ”Π»Γ40000‘Σ.
”Π»Γ40000‘Σ.
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηA≥«ΫώΡξ6‘¬ΟΩΤΫΖΫΟΉΒΡ έΦέΈΣx‘ΣΘ§ΗυΨί¬τ≥ωœύΆ§ΤΫΟΉΖΩΉ”ΒΡΒ»ΝΩΧθΦΰΘ§Ν–≥ωΖ÷ ΫΖΫ≥ΧΘ§ΫβΖ÷ ΫΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®2Θ©…η»ΞΡξ3‘¬¥”A≥«ΙΚΫχ![]() ΧΉΘ§‘ρΗυΨίΓΑ≤ΜΕύ”Ύ2224Άρ‘Σ≤Μ…Ό”Ύ2152Άρ‘ΣΒΡΉ ΫπΓ±Ν–≥ω≤ΜΒ» ΫΘ§Ϋβ≤ΜΒ» ΫΘ§ΗυΨί≤ΜΒ» ΫΒΡœό÷ΤΦ¥Ω…»ΖΕ®Ω…ΡήΖΫΑΗΘΜ
ΧΉΘ§‘ρΗυΨίΓΑ≤ΜΕύ”Ύ2224Άρ‘Σ≤Μ…Ό”Ύ2152Άρ‘ΣΒΡΉ ΫπΓ±Ν–≥ω≤ΜΒ» ΫΘ§Ϋβ≤ΜΒ» ΫΘ§ΗυΨί≤ΜΒ» ΫΒΡœό÷ΤΦ¥Ω…»ΖΕ®Ω…ΡήΖΫΑΗΘΜ
Θ®3Θ©…ηA≥«”–![]() ΧΉΘ§Ήήάϊ»σΈΣ
ΧΉΘ§Ήήάϊ»σΈΣ![]() ‘ΣΘ§Ν–≥ωA≥« έ≥ωΧΉ ΐΚΆΉήάϊ»σΒΡΙΊœΒ ΫΘ§ΉνΚσΗυΨί”κΘ®2Θ©άϊ»σœύΆ§Θ§Φ¥Ω…Ϋβ¥π.
‘ΣΘ§Ν–≥ωA≥« έ≥ωΧΉ ΐΚΆΉήάϊ»σΒΡΙΊœΒ ΫΘ§ΉνΚσΗυΨί”κΘ®2Θ©άϊ»σœύΆ§Θ§Φ¥Ω…Ϋβ¥π.
Θ®1Θ©…ηA≥«ΫώΡξ6‘¬ΟΩΤΫΖΫΟΉΒΡ έΦέΈΣx‘ΣΘ§‘ρ
![]()
Ϋβ÷°ΒΟΘΚ![]()
Ψ≠Φλ―ιΘΚ![]() «‘≠ΖΫ≥ΧΒΡΗυ.
«‘≠ΖΫ≥ΧΒΡΗυ.
¥πΘΚA≥«ΫώΡξ6‘¬ΟΩΤΫΖΫΟΉΒΡ έΦέΈΣ![]() ‘Σ.
‘Σ.
Θ®2Θ©…η»ΞΡξ3‘¬¥”A≥«ΙΚΫχ![]() ΧΉΘ§‘ρ
ΧΉΘ§‘ρ
![]()
Ϋβ÷°ΒΟΘΚ![]()
ΓύΖΫΑΗ”–ΥΡ÷÷Θ§»γœ¬±μΥυ ΨΘΚ
ΖΫΑΗ | “Μ | Εΰ | »ΐ | ΥΡ |
A≥«Θ®ΧΉΘ© | 24 | 25 | 26 | 27 |
B≥«Θ®ΧΉΘ© | 26 | 25 | 24 | 23 |
Θ®3Θ©…ηA≥«”–![]() ΧΉΘ§Ήήάϊ»σΈΣ
ΧΉΘ§Ήήάϊ»σΈΣ![]() ‘ΣΘ§‘ρ
‘ΣΘ§‘ρ
![]()
Γύ![]()
ΓΏΥυ”–ΖΫΑΗάϊ»σœύΆ§
Γύ![]() 0000‘Σ
0000‘Σ
¥πΘΚ![]() ”Π»Γ40000‘Σ.
”Π»Γ40000‘Σ.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
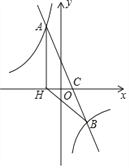
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“Μ¥ΈΚ· ΐy=ax+bΘ®aΓΌ0Θ©ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψΘ§”κx÷αΫΜ”ΎΒψCΘ§ΙΐΒψAΉςAHΓΆx÷α”ΎΒψHΘ§ΒψO «œΏΕΈCHΒΡ÷–ΒψΘ§AC=
ΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψΘ§”κx÷αΫΜ”ΎΒψCΘ§ΙΐΒψAΉςAHΓΆx÷α”ΎΒψHΘ§ΒψO «œΏΕΈCHΒΡ÷–ΒψΘ§AC=![]() Θ§tanΓœACH=2Θ§«“ΒψBΒΡΉχ±ξΈΣΘ®4Θ§nΘ©Θ°
Θ§tanΓœACH=2Θ§«“ΒψBΒΡΉχ±ξΈΣΘ®4Θ§nΘ©Θ°
Θ®1Θ©«σΗΟΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σΓςBCHΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§O «ΓςABCΒΡΆβΫ”‘≤ΒΡ‘≤–ΡΘ§ΓœABC=60ΓψΘ§BFΘ§CEΖ÷±π «ACΘ§AB±Ώ…œΒΡΗΏ«“ΫΜ”ΎΒψHΘ§CEΫΜΓ―O”ΎMΘ§DΘ§GΖ÷±π‘Ύ±ΏBCΘ§AB…œΘ§«“BD=BHΘ§BG=BOΘ§œ¬Ν–Ϋα¬έΘΚΔΌΓœABO=ΓœHBCΘΜΔΎABBC=2BFBHΘΜΔέBM=BDΘΜΔήΓςGBDΈΣΒ»±Ώ»ΐΫ«–ΈΘ§Τδ÷–’ΐ»ΖΫα¬έΒΡ–ρΚ≈ «Θ® Θ©
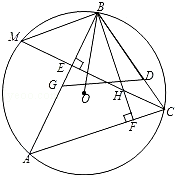
A.ΔΌΔΎ B.ΔΌΔέΔή C.ΔΌΔΎΔή D.ΔΌΔΎΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
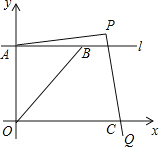
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏlΤΫ––x÷αΘ§ΫΜy÷α”ΎΒψAΘ§ΒΎ“ΜœσœόΡΎΒΡΒψB‘Ύl…œΘ§Ν§ΫαOBΘ§Ε·ΒψP¬ζΉψΓœAPQ=90ΓψΘ§PQΫΜx÷α”ΎΒψCΘ°
Θ®1Θ©Β±Ε·ΒψP”κΒψB÷ΊΚœ ±Θ§»τΒψBΒΡΉχ±ξ «Θ®2Θ§1Θ©Θ§«σPAΒΡ≥ΛΘ°
Θ®2Θ©Β±Ε·ΒψP‘ΎœΏΕΈOBΒΡ―”≥ΛœΏ…œ ±Θ§»τΒψAΒΡΉίΉχ±ξ”κΒψBΒΡΚαΉχ±ξœύΒ»Θ§«σPAΘΚPCΒΡ÷ΒΘ°
Θ®3Θ©Β±Ε·ΒψP‘Ύ÷±œΏOB…œ ±Θ§ΒψD «÷±œΏOB”κ÷±œΏCAΒΡΫΜΒψΘ§ΒψE «÷±œΏCP”κy÷αΒΡΫΜΒψΘ§»τΓœACE=ΓœAECΘ§PD=2ODΘ§«σPAΘΚPCΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΕ‘RtΓςOAB“ά¥ΈΫχ––ΈΜΥΤΓΔ÷αΕ‘≥ΤΚΆΤΫ“Τ±δΜΜΚσΒΟΒΫΓςOΓδAΓδBΓδΘ°
Θ®1Θ©‘ΎΉχ±ξ÷Ϋ…œΜ≠≥ω’βΦΗ¥Έ±δΜΜœύ”ΠΒΡΆΦ–ΈΘΜ
Θ®2Θ©…ηP(x,y)ΈΣΓςOAB±Ώ…œ»Έ“ΜΒψΘ§“ά¥Έ–¥≥ω’βΦΗ¥Έ±δΜΜΚσΒψPΕ‘”ΠΒψΒΡΉχ±ξΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”–άμ ΐaΘ§bΘ§c‘Ύ ΐ÷α…œΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§«“|a|=|c|Θ°
Θ®1Θ©»τ|a+c|+|b|=2Θ§«σbΒΡ÷ΒΘΜ
Θ®2Θ©”ΟΓΑΘΨΓ±¥”¥σΒΫ–ΓΑ―aΘ§bΘ§©¹bΘ§cΝ§Ϋ”Τπά¥Θ°
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§AΓΔBΈΣx÷α…œΝΫΒψΘ§CΓΔDΈΣy÷α…œΒΡΝΫΒψΘ§Ψ≠ΙΐΒψAΓΔCΓΔBΒΡ≈ΉΈοœΏΒΡ“Μ≤ΩΖ÷c1”κΨ≠ΙΐΒψAΓΔDΓΔBΒΡ≈ΉΈοœΏΒΡ“Μ≤ΩΖ÷c2ΉιΚœ≥…“ΜΧθΖβ±’«ζœΏΘ§Έ“Ο«Α―’βΧθΖβ±’«ζœΏ≥…ΈΣΓΑΒΑœΏΓ±Θ°“―÷ΣΒψCΒΡΉχ±ξΈΣΘ®0Θ§©¹![]() Θ©Θ§ΒψM «≈ΉΈοœΏC2ΘΚy=mx2©¹2mx©¹3mΘ®mΘΦ0Θ©ΒΡΕΞΒψΘ°
Θ©Θ§ΒψM «≈ΉΈοœΏC2ΘΚy=mx2©¹2mx©¹3mΘ®mΘΦ0Θ©ΒΡΕΞΒψΘ°
Θ®1Θ©«σAΓΔBΝΫΒψΒΡΉχ±ξΘΜ
Θ®2Θ©ΓΑΒΑœΏΓ±‘ΎΒΎΥΡœσœό…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΒΟΓςPBCΒΡΟφΜΐΉν¥σΘΩ»τ¥φ‘ΎΘ§«σ≥ωΓςPBCΟφΜΐΒΡΉν¥σ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©Β±ΓςBDMΈΣ÷±Ϋ«»ΐΫ«–Έ ±Θ§«σmΒΡ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
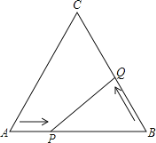
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ±Ώ≥ΛΈΣ24cmΒΡΒ»±Ώ»ΐΫ«–ΈABC÷–Θ§ΒψP¥”ΒψAΩΣ Φ―ΊAB±ΏœρΒψB“‘ΟΩΟκ÷”2cmΒΡΥΌΕ»“ΤΕ·Θ§ΒψQ¥”ΒψBΩΣ Φ―ΊBC±ΏœρΒψC“‘ΟΩΟκ÷”4cmΒΡΥΌΕ»“ΤΕ·Θ°»τPΓΔQΖ÷±π¥”AΓΔBΆ§ ±≥ωΖΔΘ§Τδ÷–»Έ“β“ΜΒψΒΫ¥οΡΩΒΡΒΊΚσΘ§ΝΫΒψΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ§«σΘΚ
Θ®1Θ©Ψ≠Ιΐ6ΟκΚσΘ§BP=ΓΓΓΓΓΓΓΓcmΘ§BQ=ΓΓΓΓΓΓΓΓcmΘΜ
Θ®2Θ©Ψ≠ΙΐΦΗΟκΓςBPQΒΡΟφΜΐΒ»”Ύ![]() ΘΩ
ΘΩ
Θ®3Θ©Ψ≠ΙΐΦΗΟκΚσΘ§ΓςBPQ «÷±Ϋ«»ΐΫ«–ΈΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§![]() «
«![]() ΒΡ±Ώ
ΒΡ±Ώ![]() …œΒΡ÷–œΏΘ°
…œΒΡ÷–œΏΘ°
Θ®1Θ©ΔΌ”Ο≥ΏΙφΆξ≥…ΉςΆΦΘΚ―”≥Λ![]() ΒΫΒψ
ΒΫΒψ![]() Θ§ Ι
Θ§ Ι![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΘΜ
ΘΜ
ΔΎ »τ![]() Θ§«σ
Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»γΆΦ2Θ§Β±![]() ±Θ§«σ÷ΛΘΚ
±Θ§«σ÷ΛΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com