
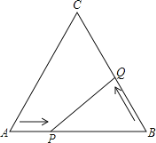
【题目】如图,在边长为24cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟2cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟4cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒△BPQ的面积等于![]() ?
?
(3)经过几秒后,△BPQ是直角三角形?
【答案】(1)12、24;(2)经过2秒△BPQ的面积等于![]() .(3)经过6秒或
.(3)经过6秒或![]() 秒后,△BPQ是直角三角形.
秒后,△BPQ是直角三角形.
【解析】
(1)根据路程=速度×时间,求出BQ,AP的值就可以得出结论;
(2)作QD⊥AB于D,由勾股定理可以表示出DQ,然后根据面积公式建立方程求出其解即可;
(3)先分别表示出BP,BQ的值,当∠BQP和∠BPQ分别为直角时,由等边三角形的性质就可以求出结论.
(1)由题意,得
AP=12cm,BQ=24cm.
∵△ABC是等边三角形,
∴AB=BC=24cm,
∴BP=224-12=12cm.
故答案为:12、24.
(2)设经过x秒△BPQ的面积等于![]() ,作QD⊥AB于D,则 BQ=4xcm.
,作QD⊥AB于D,则 BQ=4xcm.

∴∠QDB=90°,
∴∠DQB=30°,
![]()
在Rt△DBQ中,由勾股定理,得
![]()
![]()
解得;x1=10,x2=2,
∵x=10时,4x>24,故舍去
∴x=2.
答:经过2秒△BPQ的面积等于![]() .
.
(3)经过t秒后,△BPQ是直角三角形.
∵△ABC是等边三角形,
∴AB=BC=24cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,
∴∠BPQ=30°,
∴BP=2BQ.
∵BP=24-2t,BQ=4t,
∴24-2t=2×4t,
解得t=![]() ;
;
当∠QPB=90°时,
∴∠PQB=30°,
∴BQ=2PB,
∴4t=2×(24-2t)
解得t=6
∴经过6秒或![]() 秒后,△BPQ是直角三角形.
秒后,△BPQ是直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某班一次数学检测中,共出了20道题,总分为100分,现从中抽出5份试卷进行分析.如图表所示:
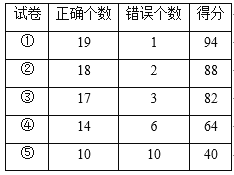
(1)某同学得了70分,他答对了试卷多少道题?
(2)有一同学H他得了76分,另一同学G说他得了72分,谁说的对了?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年3月,某炒房团以不多于2224万元不少于2152万元的资金分别从A城、B城买入小户型二手房(80平方米/套)共4000平方米.其中A城、B城的购入价格分别为4000元/平方米、7000元/平方米.自住建部今年5月约谈成都市政府负责同志后,成都市进一步加大了调控政策.某炒房团为抛售A城的二手房,决定从6月起每平方米降价1000元.如果卖出相同平方米的房子,那么5月的销售额为640万元,6月的销售额为560万元.
(1)A城今年6月每平方米的售价为多少元?
(2)请问去年3月有几种购入方案?
(3)若去年三月所购房产全部没有卖出,炒房团计划在7月执行销售方案:B城售价为1.05万元/平方米,并且每售出一套返还该购房者a元;A城按今年6月的价格进行销售。要使(2)中的所有方案利润相同,求出a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在公路 MN 两侧分别有 A![]() , A
, A![]() ......A
......A![]() ,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
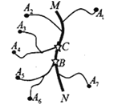
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
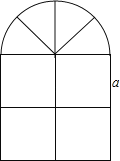
【题目】窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若数轴上![]() 两点分别对应实数
两点分别对应实数![]() ,则
,则![]() 两点之间的距离记作
两点之间的距离记作![]() ,且
,且![]() .已知点
.已知点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() .根据信息完成下列各题:
.根据信息完成下列各题:
(1)![]() =_____________.
=_____________.
(2)若数轴上点![]() 对应实数
对应实数![]() ,则
,则
①当![]() 时
时![]() =_____________;
=_____________;
②当![]() 取最小值时,
取最小值时,![]() 的取值范围为_____________.
的取值范围为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).

(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
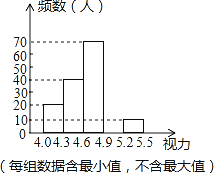
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是______事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每6个人中会有1人抽中一等奖、2人抽中二等奖,若袋中共有18个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中增加3个黄球,那么抽中一等奖的概率会怎样变化?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com