
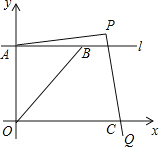
【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)当动点P在直线OB上时,点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,求PA:PC的值.
【答案】(1)PA的长为2;(2)PA:PC的值为1:1;(3)PA:PC的值为![]() 或
或![]() .
.
【解析】试题分析:(1)B点到y轴的距离是2.(2)过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,证明△ANP≌△CMP,可得PA:PC的值为1:1.(3)分类讨论,
若点P在线段OB的延长线上,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F,△ANP∽△CMP,证明四边形PMON是矩形,求出PA:PC值,若点P在线段OB的反向延长线上,,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F,同理求出比值.
试题解析:
(1)∵点P与点B重合,点B的坐标是(2,1),
∴点P的坐标是(2,1).
∴PA的长为2.
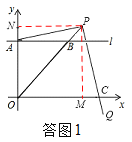
(2)如答图1,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,
∵点A的纵坐标与点B的横坐标相等,∴OA=AB.
∵∠OAB=90°,∴∠AOB=∠ABO=45°.
∵∠AOC=90°,∴∠POC=45°.
∵PM⊥x轴,PN⊥y轴,∴PM=PN,∠ANP=∠CMP=90°.∴∠NPM=90°.
∵∠APC=90°.∴∠APN=90°∠APM=∠CPM.
在△ANP和△CMP中,∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP,
∴△ANP≌△CMP.∴PA=PC.∴PA:PC的值为1:1.
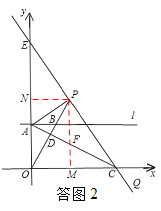
(3)①若点P在线段OB的延长线上,如答图2,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F.
∵∠APN=∠CPM,∠ANP=∠CMP,∴△ANP∽△CMP.∴ ![]() .
.
∵∠ACE=∠AEC,∴AC=AE.
∵AP⊥PC,∴EP=CP.
∵PM∥y轴,∴AF=CF,OM=CM.∴FM= ![]() OA.
OA.
设OA=x,∵PF∥OA,∴△PDF∽△ODA.∴ ![]() .
.
∵PD=2OD,∴PF=2OA=2x,FM= ![]() x.∴PM=
x.∴PM= ![]() x.
x.
∵∠APC=90°,AF=CF,∴AC=2PF=4x.
∵∠AOC=90°,∴OC= ![]() x.
x.
∵∠PNO=∠NOM=∠OMP=90°,∴四边形PMON是矩形.∴PN=OM= ![]() x.
x.
∴PA:PC=PN:PM= ![]() x:
x: ![]() x=
x= ![]() .
.
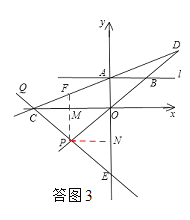
②若点P在线段OB的反向延长线上,如答图3,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F.
同理可得:PM= ![]() x,CA=2PF=4x,OC=
x,CA=2PF=4x,OC= ![]() x.
x.
∴PN=OM= ![]() OC=
OC= ![]() x.
x.
∴PA:PC=PN:PM= ![]() x:
x: ![]() x=
x= ![]() .
.
综上所述:PA:PC的值为![]() 或
或 ![]() .
.


科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;②西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(![]() ):
):
(1)若该客户按方案①购买,需付款______________元(用含x的代数式表示);若该客户按方案②购买,需付款________________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班一次数学检测中,共出了20道题,总分为100分,现从中抽出5份试卷进行分析.如图表所示:
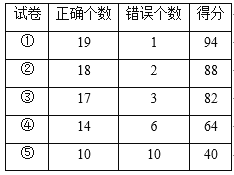
(1)某同学得了70分,他答对了试卷多少道题?
(2)有一同学H他得了76分,另一同学G说他得了72分,谁说的对了?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
科目:初中数学 来源: 题型:
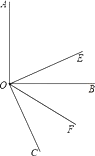
【题目】如图,已知∠AOB是直角,OE平分∠AOC,OF平分∠BOC.
(1)若∠BOC=60°,求∠EOF的度数;
(2)若∠AOC=x°(x>90),此时能否求出∠EOF的大小,若能,请求出它的数值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
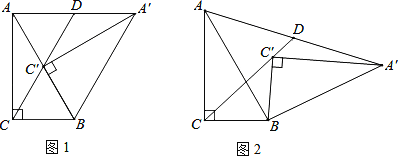
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年3月,某炒房团以不多于2224万元不少于2152万元的资金分别从A城、B城买入小户型二手房(80平方米/套)共4000平方米.其中A城、B城的购入价格分别为4000元/平方米、7000元/平方米.自住建部今年5月约谈成都市政府负责同志后,成都市进一步加大了调控政策.某炒房团为抛售A城的二手房,决定从6月起每平方米降价1000元.如果卖出相同平方米的房子,那么5月的销售额为640万元,6月的销售额为560万元.
(1)A城今年6月每平方米的售价为多少元?
(2)请问去年3月有几种购入方案?
(3)若去年三月所购房产全部没有卖出,炒房团计划在7月执行销售方案:B城售价为1.05万元/平方米,并且每售出一套返还该购房者a元;A城按今年6月的价格进行销售。要使(2)中的所有方案利润相同,求出a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在公路 MN 两侧分别有 A![]() , A
, A![]() ......A
......A![]() ,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
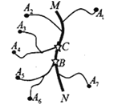
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
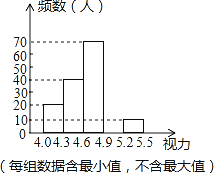
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com