
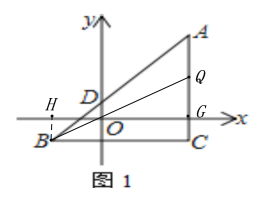
【题目】△ABC在平面直角坐标系内如图1摆放,A、C两点的横坐标都是5,BC∥x轴.已知B点坐标为(-3,m),AB交y轴于点D,且AC=BC.
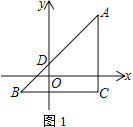
(1) 填空:BC=_____;△ABC的面积为______;用m表示点A的坐标为______.
(2) 射线BO交直线AC于点Q,若△ABQ的面积为16,试求m的值
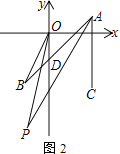
(3) 如图2,点D在y轴负半轴上,∠BAC的三等分线AP与∠BOD的角平分线OP交于点P,其中∠BAC=3∠BAP=45°.若∠P>2∠B,试求∠BOD的取值范围.
【答案】(1)8,32,(5,m+8);(2)m=![]() 或m=
或m=![]() (3)40°<∠BOD<45°.
(3)40°<∠BOD<45°.
【解析】
(1)根据A、C点横坐标为5,说明AC⊥x轴,根据与x轴,y轴平行的直线上点坐标特征确定点A坐标,再根据面积公式求解;
(2)通过证明三角形相似,利用其性质表示出Q点的坐标,再根据面积公式列方程求解;
(3)设∠BOP=∠POD=α,利用外角等于不相邻两个内角和及已知角的关系将∠P和∠B用α表示,根据题意列不等式求α的解集,再结合外角大于任何一个不相邻的内角确定∠BOD的范围.
解:(1)∵A、C点横坐标为5,B点坐标为(-3,m),
∴BC=5-(-3)=8,
∵BC∥x轴,
∴∠ACB=90°
∵AC=BC
∴S△ABC=![]()
∵B (-3,m), BC=AC=8,
∴A(5,m+8);
(2)如图,过B作BH⊥x轴,垂足为H,AC与x轴交于点G,
∴∠BHO=∠QGO=90°, ∠HOB=∠GOQ,
∴△HOB∽△GOQ,
∴![]() ,
,
∴![]() ,
,
∴QG=![]() ,
,
∴Q的坐标为![]() ,
,
∴AQ的长度为![]() ,
,
∵△ABQ的面积为16,
∴![]() ,
,
解得:m=![]() 或m=
或m=![]() .
.
(3)如图,AP与y轴交于点N,点M在y轴上,
∵OP是∠BOD的角平分线,
∴∠BOP=∠POD,
∵∠ACB=90°,AC=BC,
∴∠BAC=∠ABC=45°,
∵∠BAC=3∠BAP=45°
∴∠BAP=15°, ∠CAP=30°,
∵OM∥AC,
∴BDM=∠BAC=45°, ∠PNM=∠PAC=30°,
设∠BOP=∠POD=α,
∵∠BDM=∠B+∠BOD,
∴∠B=∠BDM-∠BOD=45°-2α,
∵∠PNM=∠POM+∠P,
∴∠P=∠PNM-∠POM=30°-α,
∵∠P>2∠B,
∴30°-α>2(45°-2α)
解得,α>20°
∴∠BOD>40°
∵∠BDM >∠BOD,
∴∠BOD<45°
∴40°<∠BOD<45°.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】重庆出租车计费的方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车起步价是_____元;
(2)当x>2时,求y与x之间的关系式;
(3)若某乘客一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 |
|
二 |
| 10 | 0.2 |
三 |
| 12 |
|
四 |
|
| 0.4 |
五 |
| 6 |
|

请根据表格提供的信息,解答以下问题:
(1)本次决赛共有__________名学生参加;
(2)直接写出表中:![]() ___________
___________![]() ____________
____________
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.(售价不低于进价).请根据小丽提供的信息,解答小华和小明提出的问题.

认真阅读上面三位同学的对话,请根据小丽提供的信息.
(1)解答小华的问题;
(2)解答小明的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校随机选取40名学生进行军运会知识考查,对考查成绩进行统计(成绩均为整数),并依据统计数据绘制了如下统计图表.解答下列问题:
组别 | 分数段/分 | 频数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |

(1) 表中a=______;b=______;c=____;
(2) 请补全频数分布直方图;
(3) 已知该学校共有学生1280人,若考查成绩80分以上(不含80分)为优秀,试估计该学校学生军运会知识考查成绩达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=75°,BC=7,△ABC的面积为14,D为 BC边上一动点(不与B,C重合),将△ABD和△ACD分别沿直线AB,AC翻折得到△ABE与△ACF,那么△AEF的面积最小值为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
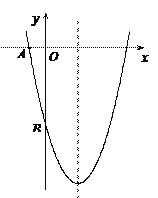
【题目】如图,已知二次函数![]() 的图象与坐标轴交于点A(-1, 0)和点B(0,-5).
的图象与坐标轴交于点A(-1, 0)和点B(0,-5).
(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com