练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】观察下列各式：

    =-1；

    ；

    .

    （1）根据前面各式的规律可得：

    ①.

    ②.

    （2）请用上面的结论进行计算：

    ①（答案可含有幂的形式表示）；

    ②若，求的值.

    【答案】（1）①；②;（2）①；②.

    【解析】

    （1）①由=-1；

    ；

    发现：等号右侧x的指数等于左侧的第二个括号内次数最高的指数加1 ，然后再减去1即可.

    故；

    ②通过①的规律可得：；

    （2）①通过观察将×（-2-1）可得到上述规律，最后再÷（-2-1）即可；

    ②通过观察利用等式的基本性质将原方程两边同时乘（x-1）方程左侧得出以上规律，解方程即可.

    （1）①由=-1；

    ；

    发现：等号右侧x的指数等于左侧的第二个括号内次数最高的指数加1 ，然后再减去1即可.

    故；

    ②通过①的规律可得：；

    （2）①原式=

    =

    =；

    ②将原方程两边同时乘（x-1）得：

    故.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，正比例函数与反比例函数的图象分别交于A、C两点，已知点B与点D关于坐标原点O成中心对称，且点B的坐标为其中．

    四边形ABCD的是______填写四边形ABCD的形状

    当点A的坐标为时，四边形ABCD是矩形，求m，n的值．

    试探究：随着k与m的变化，四边形ABCD能不能成为菱形？若能，请直接写出k的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某乡村距城市50km,甲骑自行车从乡村出发进城，出发1小时30分后，乙骑摩托车也从乡村出发进城，结果比甲先到1小时，已知乙的速度是甲的2.5倍，求甲、乙两人的速度。

    【答案】甲速12km/h,乙速30km/h.

    【解析】试题分析：设甲的速度是则乙的速度是甲、乙所用时间分别为: 小时、小时;根据题意可得甲比乙多用2.5小时,从而可得关于的方程,解方程即可解答此题;注意,最后要结合题意验根.

    试题解析：设甲的速度是则乙的速度是 根据题意列方程,得

    整理,得

    ，

    解得：

    经检验, 是原方程的解.

    则

    答:甲的速度是12km/h,乙的速度是30km/h.

    【题型】解答题
    【结束】
    24

    【题目】已知求的值 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

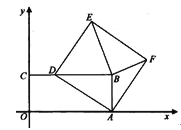
    【题目】如图，在平面直角坐标系xoy中，矩形OABC的顶点B坐标为（12,5)，点D在 CB边上从点C运动到点B，以AD为边作正方形ADEF，连BE、BF，在点D运动过程中，请探究以下问题：

    (1)△ABF的面积是否改变，如果不变，求出该定值；如果改变，请说明理由；

    (2)若△BEF为等腰三角形，求此时正方形ADEF的边长；

    (3)设E(x,y)，直接写出y关于x的函数关系式及自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，BE∥DF，∠DBE和∠CDF的角平分线交于点G．当∠BGD＝65°时，∠BDC＝________度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC在平面直角坐标系内如图1摆放，A、C两点的横坐标都是5，BC∥x轴．已知B点坐标为(－3，m)，AB交y轴于点D，且AC＝BC.

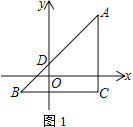
    (1) 填空：BC＝_____；△ABC的面积为______；用m表示点A的坐标为______.

    (2) 射线BO交直线AC于点Q，若△ABQ的面积为16，试求m的值

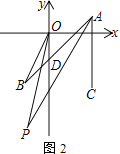
    (3) 如图2，点D在y轴负半轴上，∠BAC的三等分线AP与∠BOD的角平分线OP交于点P，其中∠BAC＝3∠BAP＝45°．若∠P＞2∠B，试求∠BOD的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

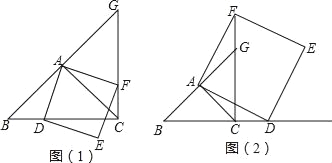
    【题目】在△ABC中，AB=AC，∠BAC=90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与直线CF相交于点G．

    （1）若点D在线段BC上，如图（1），判断：线段BC与线段CG的数量关系：　 　，位置关系：　 　．

    （2）如图（2），①若点D在线段BC的延长线上，（1）中判断线段BC与线段CG的数量关系与位置关系是否仍然成立，并说明理由；

    ②当G为CF中点，连接GE，若AB=，求线段GE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线射线，。是射线上一动点，过点作交射线于点，连结。作，交直线于点，平分。

    （1）若点都在点的右侧。

    ①求的度数；

    ②若，求的度数。

    （2）在点的运动过程中，是否存在这样的情形，使，若存在，求出的度数；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中，真命题有（　　）①同旁内角互补；②长度为2、3、5的三条线段可以构成三角形；③平方根、立方根是它本身的数是0和1；④和﹣|﹣2|互为相反数；⑤4＜＜5；⑥在同一平面内，如果a∥b，a⊥c．那么b⊥c．

    A.0个B.1个C.2个D.3个

    查看答案和解析>>

    同步练习册答案