
如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.
(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.
(2)引申:如果∠C 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____度时,图中阴影部分的面积和有最大值是________.

(1)证明见解析;(2)成立,证明见解析;(3)18.
【解析】
试题分析:(1)因为AC=DC,∠ACB=∠DCF=90°,BC=FC,所以△ABC≌△DFC,从而△ABC与△DFC的面积相等;
(2)延长BC到点P,过点A作AP⊥BP于点P;过点D作DQ⊥FC于点Q.得到四边形ACDE,BCFG均为正方形,AC=CD,BC=CF,∠ACP=∠DCQ.所以△APC≌△DQC.于是AP=DQ.又因为S△ABC=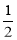 BC•AP,S△DFC=
BC•AP,S△DFC=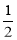 FC•DQ,所以S△ABC=S△DFC;
FC•DQ,所以S△ABC=S△DFC;
(3)根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.所以S阴影部分面积和=3S△ABC=3×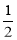 ×3×4=18.
×3×4=18.
试题解析:(1)证明:在△ABC与△DFC中,
∵ ,
,
∴△ABC≌△DFC.
∴△ABC与△DFC的面积相等;
(2)【解析】
成立.理由如下:
如图,延长BC到点P,过点A作AP⊥BP于点P;过点D作DQ⊥FC于点Q.
∴∠APC=∠DQC=90°.
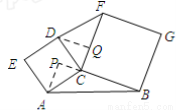
∵四边形ACDE,BCFG均为正方形,
∴AC=CD,BC=CF,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,
∴∠ACP=∠DCQ.
∴ ,
,
△APC≌△DQC(AAS),
∴AP=DQ.
又∵S△ABC=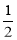 BC•AP,S△DFC=
BC•AP,S△DFC=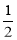 FC•DQ,
FC•DQ,
∴S△ABC=S△DFC;
(3)【解析】
根据(2)得图中阴影部分的面积和是△ABC的面积三倍,
若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,
∴当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.
∴S阴影部分面积和=3S△ABC=3×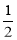 ×3×4=18.
×3×4=18.
考点:四边形综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:选择题
如图,A、B、C是反比例函数 (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
A.4条 B.3条 C.2条 D.1条

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:解答题
如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是
,那么点B′的坐标是

A.(-2,3) B.(2,-3) C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
抛物线 可以由抛物线
可以由抛物线 平移得到,则下列平移过程正确的是
平移得到,则下列平移过程正确的是
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点A坐标为(-1,0).则下面的四个结论:①2a+b=0;②4a+2b+c>0 ③B点坐标为(4,0);④当x<-1时,y>0.其中正确的是

A.①② B.③④ C.①④ D.②③
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省临沂市九年级中考一模数学试卷(解析版) 题型:选择题
拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学记数法表示为( )
A.0.5×1011千克 B.50×109千克 C.5×109千克 D.5×1010千克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com