
����Ŀ����ͼ1����֪������y=��x2+bx+c��x�ύ��A����1��0����B���㣬����A�ڵ�B����ࣩ����ֱ��AC���ڵ�C��2��3����ֱ��AC�������ߵĶԳ���l�ཻ�ڵ�D������BD��
��1���������ߵĺ�������ʽ���������D�����ꣻ
��2����ͼ2������M��Nͬʱ�ӵ�D����������ÿ��1����λ���ȵ��ٶȷֱ���DA��DB�˶�������MN������DMN��MN���ۣ��õ���D��MN���ж��ı���DMD��N����״����˵�����ɣ����˶�ʱ��tΪ��ֵʱ����D��ǡ������x���ϣ�
��3����ƽ���ڣ��Ƿ���ڵ�P������A�㣩��ʹ����P��B��DΪ��������������ABD���ƣ�ȫ�ȳ��⣩�������ڣ���ֱ��д����P�����꣬�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����A����1��0����C��2��3������y=��x2+bx+c���ã�
![]() ��
��
��ã� ![]() ��
��
�������ߵĽ���ʽΪy=��x2+2x+3��
��y=��x2+2x+3=����x��1��2+4��
�������ߵĶԳ���Ϊֱ��x=1��
��ֱ��AC�ĺ�������ʽΪy=kx+b��
��A����1��0����C��2��3������y=kx+b���ã�
![]() ��
��
��ã� ![]() ��
��
��ֱ��AC�ĺ�������ʽΪy=x+1��
�֡ߵ�D��ֱ��AC�������ߵĶԳ���Ľ��㣬
��xD=1��yD=1+1=2��
���D��������1��2��
��2��
�⣺�ı���DMD��N�������Σ��������£�
��������y=��x2+2x+3��x�ύ��A��B���㣬
����y=0���é�x2+2x+3=0��
��ã�x1=��1��x2=3��
��A����1��0����B��3��0����
��AD= ![]() =2
=2 ![]() ��BD=
��BD= ![]() =2
=2 ![]() ��AB=1+3=4��
��AB=1+3=4��
��AD2+BD2=AB2��
���ABD�ǵ���ֱ�������Σ�
���DAB=��DBA=45�㣬��ADB=90�㣬
�ɷ��ۿ�֪��D��M=DM��DN=ND�䣬
�֡�DM=DN��
���ı���MDND��Ϊ���Σ�
�ߡ�MDN=90�㣬
���ı���MDND���������Σ�
��DM=DN=t������D����x���ϵĵ�D�䴦ʱ��
���ı���MDND��Ϊ�����Σ�
���D��NB=90�㣬
��Rt��D��NB��D��N=t��BN=2 ![]() ��t��BD��=2��
��t��BD��=2��
��t2+��2 ![]() ��t��2=22��
��t��2=22��
��t1=t2= ![]() ��
��
�������� ![]() sʱ����Dǡ������x���ϵ�D�䴦
sʱ����Dǡ������x���ϵ�D�䴦
��3��
�⣺���ڣ�
��ͼ��

�ɣ�2��֪��ABDΪ����ֱ�������Σ�
�ߡ�PBD���ABD���ƣ��Ҳ�ȫ�ȣ�
���PBD����BDΪб�ߵĵ���ֱ�������Σ�
���P��������1��0����2��3��
����������1�������ô���ϵ������������ߺ�ֱ�ߵĽ���ʽ���Ӷ��ó��Գ�����ֱ�ߵĽ��㣻��2���������߽���ʽ��õ�A��B���꣬��ϵ�D�����֪��ABDΪ����ֱ�������Σ�����DAB=��DBA=45�㡢��ADB=90�㣬�ɷ������ʵ�D��M=DM��DN=ND�䣬�Ӷ��ó��ı���MDND��Ϊ���Σ����ݡ�MDN=90�㼴�ɵ��ı���MDND��Ϊ�����Σ���DM=DN=t����Rt��D��NB��D��N=t��BN=2 ![]() ��t��BD��=2�����ݹ��ɶ������ɵó�t��ֵ����3���ɡ�ABDΪ����ֱ�������μ���PBD���ABD�����Ҳ�ȫ�ȣ�֪��PBD����BDΪб�ߵĵ���ֱ�������Σ����ͼ�μ��ɵô𰸣�
��t��BD��=2�����ݹ��ɶ������ɵó�t��ֵ����3���ɡ�ABDΪ����ֱ�������μ���PBD���ABD�����Ҳ�ȫ�ȣ�֪��PBD����BDΪб�ߵĵ���ֱ�������Σ����ͼ�μ��ɵô𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y=��x2+2bx+c��x�ύ�ڵ�A��B����A�ڵ�B���Ҳࣩ������y�������ύ�ڵ�C����֪A��2��0�� 
��1����B����4��0��ʱ���������ߵĽ���ʽ��
��2��OΪ����ԭ�㣬�����ߵĶ���ΪP����tan��OAP=3ʱ����������ߵĽ���ʽ��
��3��OΪ����ԭ�㣬��AΪԲ��OA��Ϊ�뾶����A����CΪԲ�ģ� ![]() OC��Ϊ�뾶��Բ��C������A���C����ʱ����������ߵĽ���ʽ��
OC��Ϊ�뾶��Բ��C������A���C����ʱ����������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ��x��ֱ���A��B���㣨��B�ڵ�A���ұߣ���P�ǰ뾶OB��һ�㣬��P�Ҵ�ֱ��AB��ֱ�����O�ֱ���C��D���㣨��C�ڵ�D���Ϸ�����ֱ��AC��DB���ڵ�E����AC��CE=1��2�� 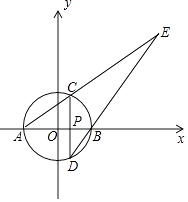
��1�����P�����ꣻ
��2�������A�͵�E���Ҷ�����ֱ��CD�ϵ������ߵĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ŀ������![]() ������ϵ����
������ϵ����![]() ��ӡˢ�������
��ӡˢ�������
��1��������![]() ���³�3�����㻯��3x2+6x+8���C��6x+5x2+2����
���³�3�����㻯��3x2+6x+8���C��6x+5x2+2����
��2��������˵������´��ˣ��ҿ���������𰸵Ľ���dz�������ͨ������˵��ԭ������![]() ���Ǽ���
���Ǽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ��������B����O������BM����CD��BM����AB�ڵ�F����![]() =
=![]() ������AC��AD���ӳ�AD��BM�ڵ�E��
������AC��AD���ӳ�AD��BM�ڵ�E��
��1����֤����ACD�ǵȱ�������.
��2������OE����DE=2����OE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽƬABCD�У�AD=4cm����E��F�ֱ���CD��AB���е㣬�ֽ�����ֽƬ�۵���ʹ��B����EF�ϵĵ�G�����ۺ�ΪAH����HG�ӳ���ǡ�þ�����D����CD�ij�Ϊ�� �� 
A.2cm
B.2 ![]() cm
cm
C.4cm
D.4 ![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ABCD�Ķ���B��C��x���ϣ�A��D����ֱ��ڷ���������y=�� ![]() ��x��0����y=
��x��0����y= ![]() ��x��0����ͼ���ϣ���ABCD�����Ϊ ��
��x��0����ͼ���ϣ���ABCD�����Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��������ʾ��һ����˺Ȱ��ͶȰƺ�1.5Сʱ����ѪҺ�оƾ�����y������/�ٺ�������ʱ��x��ʱ���Ĺ�ϵ�ɽ��Ƶ��ö��κ���y=��200x2+400x�̻���1.5Сʱ����1.5Сʱ��y��x�ɽ��Ƶ��÷���������y= ![]() ��k��0���̻�����ͼ��ʾ����
��k��0���̻�����ͼ��ʾ���� 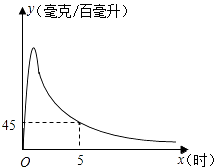
��1������������ѧģ�ͼ��㣺 �ٺȾƺ�ʱѪҺ�еľƾ������ﵽ���ֵ�����ֵΪ���٣�
�ڵ�x=5ʱ��y=45����k��ֵ��
��2�������ҹ涨��������ʻ��ԱѪҺ�еľƾ��������ڻ����20����/�ٺ���ʱ���ڡ��ƺ��ʻ�������ܼݳ���·������������ѧģ�ͣ�����ij��ʻԱ����20��00�ڼҺ�����ͶȰƣ��ڶ�������7��00�ܷ�ݳ�ȥ�ϰࣿ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����E��F�ֱ���AB��AC�ϣ�AE=AF��BF��CE�ཻ�ڵ�P����֤��PB=PC����ֱ��д��ͼ��������ȵ��߶Σ� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com