练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在等腰△ABC中，底边BC=20cm，三角形的面积为
    100
    		3
    3
    cm2，求这个等腰三角形的底角度数．
    考点：解直角三角形
    专题：计算题
    分析：过A作AD⊥BC，利用三线合一得到AD垂直于BC，BD=CD，根据已知面积，由BC的长求出AD的长，在直角三角形ABD中，利用锐角三角函数定义求出tanB的值，即可确定出∠B的度数．
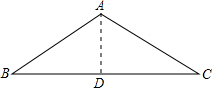    解答：解：过A作AD⊥BC，利用三线合一得到AD平分∠BAC，BD=CD=
    1
    2
    BC=10cm，
    ∵三角形的面积为
    100
    		3
    3
    cm2，即S=
    1
    2
    BC•AD=10AD=
    100
    		3
    3
    ，
    ∴AD=
    10
    		3
    3
    cm，
    在Rt△ABD中，tanB=
    AD
    BD
    =
    10
    		3
    3
    10
    =
    		3
    3
    ，
    则∠B=30°，即这个等腰三角形的底角度数30°．
    点评：此题考查了解直角三角形，涉及的知识有：等腰三角形“三线合一”性质，锐角三角函数定义，以及特殊角的三角函数值，熟练掌握直角三角形的性质是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    计算：
    （1）（3x-2y）2-（3x-y）（3x+y）；      
    （2）x2（x-1）+2x（x2-2x+3）；
    （3）（10x4-15x2-5x）÷（-5x）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    两条直线被第三条直线所截，∠1是∠2的同旁内角，∠3是∠2的内错角．
    （1）画出示意图；
    （2）若∠1=3∠2，∠2=3∠3，求∠1，∠2的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，AB=AC，
    （1）若tan
    ∠BAC
    2
    =
    1
    2
    ，求sin∠BAC的值；
    （2）若tan∠BAC=
    3
    4
    ，求sin
    ∠BAC
    2
    的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    2013年开始，国家在113个环境保护重点城市和国家环境保护模仿城市开展PM2.5的检测工作并发布检测信息．“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物．某日随机抽取25个城市检测点的研究性数据，并绘制成统计表和扇形统计图如下：
    类别组别PM2.5日平均浓度值（微克/立方米）频数频率
    A115～3020.08
    230～4530.12
    B345～60ab
    460～7550.20
    C575～906c
    D690～10540.16
    　　　　　　　　　　 合计以上分组均含最小值，不含最大值251.00
    根据图表中提供的信息解答下列问题：
    （1）统计表中的a=
     
    ，b=
     
    ，c=
     
    ；
    （2）在扇形统计图中，A类所对应的圆心角是
     
    度；
    （3）我国PM2.5安全值的标准采用世卫组织（WHO）设定的最宽限值：日平均浓度小于75微克/立方米．请你估计当日环保监测中心在检测100个城市中，PM2.5日平均浓度值符合安全值的城市约有多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在?ABCD中，对角线AC，BD相交于点O，AD=3
    		3
    ，BD=6，AC=12，求?ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

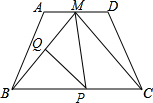    如图，在等腰梯形ABCD中，AD∥BC，M是AD的中点，BC=8，MB=5
    （1）判断△MBC的形状，并说明理由
    （2）若点P，Q分别是线段BC，BM上的动点（点P与点B，C均不重合），且∠MPQ=∠MCB，设BP=x，QM=y，求y与x的关系式及x的取值范围，判断y是否存在最大（或最小）值？若存在，求出其值，并判断此时△MQP的形状；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠C=90°，AC=2，BC=1，则cosA的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，在四边形ABCD中，以AC为斜边作Rt△ACE，且∠BED为直角．求证：四边形ABCD是矩形．

    查看答案和解析>>

    同步练习册答案