
 已知,AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,求△PCD的面积的最小值是多少?
已知,AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,求△PCD的面积的最小值是多少?| OP |
| PQ |
| OG |
| GH |
 解:∵CD是定值,所以当P到CD的距离最小时△PCD的面积最小,
解:∵CD是定值,所以当P到CD的距离最小时△PCD的面积最小,| 1 |
| 2 |
| 1 |
| 2 |
| OP |
| PQ |
| OG |
| GH |
| 2 |
| PQ |
| 2.5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求:
如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求:查看答案和解析>>
科目:初中数学 来源: 题型:
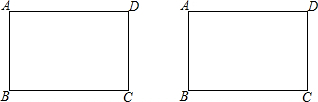 某自然景区有一块长12米,宽8米的矩形花圃(如图所示),喷水无安装在矩对角线的交点P上,现计算从P点引3条射线,把花圃分成面积相等的三部分,分别种植三种不同的花,如果不考虑分不分的间隙.
某自然景区有一块长12米,宽8米的矩形花圃(如图所示),喷水无安装在矩对角线的交点P上,现计算从P点引3条射线,把花圃分成面积相等的三部分,分别种植三种不同的花,如果不考虑分不分的间隙.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.
如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com