
 如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.
如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
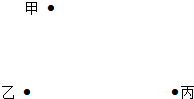 作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)
作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com