
����Ŀ��ij���Ϊ��ӭ�ӡ�����ڡ��ƶ��˻�ƻ����¾����鿴�ƻ��鷢�֣�A��ͼ��ı����B��ͼ���۵�1.5�������˿���1080Ԫ����ͼ�飬�ܵ�������A��ͼ�������ǡ�ñȵ�������B��ͼ���������20��.�����A��B����ͼ��ı��.
���𰸡�A��27Ԫ�� B:18Ԫ
�������������������B��ͼ��ı����xԪ����A��ͼ��ı����1.5xԪ��������1080Ԫ����ͼ�飬��������A��ͼ�������ǡ�ñȵ�������B��ͼ���������20���г���ʽ������⼴�ɣ�
���������
�⣺��B��ͼ��ı����xԪ����A��ͼ��ı����1.5xԪ��
��������ã� ![]() ��
��
ȥ��ĸ�ã�1620��1080��30x��
��ã�x��18��
������x��18��ԭ��ʽ���̵Ľ⣬
1.5x��27��
��A��B����ͼ��ı�۷ֱ�Ϊ27Ԫ��18Ԫ��
�����͡������
��������
25
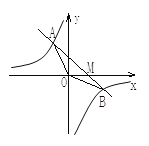
����Ŀ����ͼ,��֪һ�κ���y1=kx+b��ͼ���뷴��������![]() ��ͼ����A��B����, �ҵ�A������Ϊ��-2,3������B����������-2,��:
��ͼ����A��B����, �ҵ�A������Ϊ��-2,3������B����������-2,��:
(1)һ�κ����뷴���������Ľ���ʽ;
��2������ͼ��ָ������![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() >
>![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]()
��3������ͼ��ָ������![]() >3ʱ
>3ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�������
�������������������1����A��������뷴������������ʽ���m��ֵ����B�����������뷴������������ʽ���B��ĺ����꣬�ٰ�A��B������������һ�κ�������ʽ���k��b��ֵ���ɣ�
��2������A��B�ĺ����꣬���ͼ�ɵó�����
��3�����x��3ʱy2��ֵ��Ȼ����ͼ�ɵó�y2��ȡֵ��Χ��
���������
�⣺��1����A����2��3���ڷ���������y2��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��m����2��3
����6��
�������������Ľ���ʽΪy2��![]() ��
��
��y2����2ʱ��x��3��
��B��3����2����
��A����2��3����B��3����2������y��kx��b�ã�
![]() ��
��
��ã� ![]() ��
��
��һ�κ����Ľ���ʽΪy����x��1��
��2�����ͼ��ɵ�y1��y2ʱ��Ӧ��ͼ���ڵ�A������y�����B֮�䣬
��x����2��0��x��3��
ͬ��y1��y2ʱ��Ӧ��ͼ���ڵ�A��y��֮��͵�B���Ҳ࣬
����2��x��0��x��3��
��3����x��3ʱ��y2����2��
��x��3ʱ������������Ӧ��ͼ���ڵ�B���Ҳಿ�֣�
��Ӧ�ĺ���ֵ��2��y2��0��


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ż������ͼ����ʾ�Ĺ���������ȥ����������ʵ���ԣ�a��b����ʾ��a�еĵ�b�������磨3��2����ʾż��10��
��1��ͼ�У�8��4����λ�ñ�ʾ������________��ż��42��Ӧ������ʵ������________
��2����n�е����һ�����ú�n�Ĵ���ʽ��ʾΪ________������Ҫ˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����Ϊ18cm��ϸ��Χ��һ������������.
��1����������ǵױ߳���2�����������θ��ߵij���
��2����Χ����һ�ߵij���4cm�ĵ��������������ܣ�����������ߵij��������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������:
��1��![]() (2)
(2) ![]()
(3) ![]() (4)
(4) 
���𰸡�(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ; (4)
; (4) ![]()
�������������������1�����ӡ���ĸ�ֽ���ʽ��Լ�ּ��ɣ�
��2����ͨ�ּ��������ڷ�ʽ�ļ�����Ȼ��ѳ���ת��Ϊ�˷������ӡ���ĸ�ֽ���ʽ��Լ�ּ��ɣ�
��3���ڶ�����ʽ���ӡ���ĸ�ֽ���ʽ��Լ�֣�Ȼ��ͨ��ת��Ϊͬ��ĸ��ʽ���������ͬ��ĸ��ʽ�ļӼ�������㼴�ɣ�
��4����ͨ�ּ��������ڷ�ʽ�ļ�����Ȼ��ѳ���ת��Ϊ�˷������ӡ���ĸ�ֽ���ʽ��Լ�ּ��ɣ�
���������
�⣺��1��ԭʽ��
��![]() ��
��
��2��ԭʽ��![]()
��![]()
��![]() ��
��
��3��ԭʽ��![]()
��![]()
��![]()
��![]()
��![]() ��
��
��4��ԭʽ��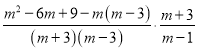
��![]()
��![]() ��
��
�㾦�����⿼���˷�ʽ�Ļ�����㣬�����������㷨�������˳���ǽⱾ��Ĺؼ���
�����͡������
��������
20
����Ŀ�����ʽ���̣�
(1) ![]() (2)
(2) ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������ѧ�����Ա���Գ�һ�����������������꼶��ѧ������������Ϊ2��3��5����ͼ��ʾ������ͼ��ʾ�����ֲ��������֪���Գ�һ��ѧ��Ϊ10�ˣ�������˵������ȷ���ǣ�������

A. ���μ�Բ�Ľ���72�� B. ѧ������������90��
C. �����������ȳ�����������10�� D. ��һ�������ȳ�����������15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����
��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ��3��
��3��
��![]() ����������Ϊ2��С������Ϊ
����������Ϊ2��С������Ϊ![]() ��2��
��2��
��1��![]() ��1��2
��1��2
��![]() ��1����������Ϊ1��
��1����������Ϊ1��
��![]() ��1��С������Ϊ
��1��С������Ϊ![]() ��2
��2
������⣺��֪��a��![]() ��3���������֣�b��
��3���������֣�b��![]() ��3��С�����֣�
��3��С�����֣�
��1��a��b��ֵ��
��2������a��3+��b+4��2��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ����Ĵ�ֱƽ���߷ֱ�AB��BD��BC�ڵ�E��F��G������ED��DG��
��1�����ж��ı���EBGD����״����˵�����ɣ�
��2������ABC=30�㣬��C=45�㣬ED=2 ![]() ����H��BD�ϵ�һ�����㣬��HG+HC����Сֵ��
����H��BD�ϵ�һ�����㣬��HG+HC����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ж�AB��CD�������У� ������
��1����B+��BCD=180������2����1=��2����3����3=��4����4����B=��5��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com