练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图所示，设A B，C，D是四个养猪场，现要建一座饲料加工厂，并且饲料加工厂到A，B，C，D各修-条公路．小明的爸爸承包了这项工程，为了节省资金，他请同学们给他设计道路施工方案．
    （1）饲料厂应建在什么位置？
    （2）试用数学知识说明你的设计理由．

    分析 （1）连接BD，AC与BD的交点就是P点位置；
    （2）根据线段的性质：两点之间，线段距离最短；结合题意，要使它与四个养猪场的距离之和最小，就要使他在AC与BD的交点处．

    解答 解：（1）如图所示：

    （2）理由：由线段的性质：两点之间，线段距离最短，
    即可得出AP+PC+BP+DP=AC+BD最小，此时最节省资金．

    点评 本题考查了应用设计与作图，结合线段的性质：两点之间，线段距离最短是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．安徽省2014年全国粮食总产约683.2亿斤，用科学记数法表示683.2亿正确的是（　　）
    A．68.32×1010B．6.832×1010C．683.2×1011D．6.832×1011

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．（一）观察如图，回答下列问题：

    （1）图（2）中共有3条线段；
    （2）图（4）中共有10条线段；所有线段长度的和是20；
    （3）按这样的规律画下去，到图（7）时，所有线段长度的和是84；
    （二）观察下列等式：
    1×1=$\frac{1×2×3}{6}$；
    1×2+2×1=$\frac{2×3×4}{6}$；
    1×3+2×2+3×1=$\frac{3×4×5}{6}$；
    1×4+2×3+3×2+4×1=$\frac{4×5×6}{6}$；
    …
    请你将想到的规律用含有 n（n是正整数）的等式来表示就是：1×n+2×（n-1）+…+（n-1）×2+n×1=$\frac{n（n+1）（n+2）}{6}$．
    猜想：在问题（一）中，按规律画下去，到图（100）时，所有线段长度的和是171700．

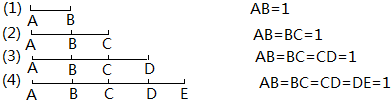
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

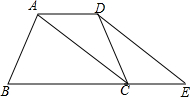    16．如图，在梯形ABCD中，AD∥BC，CA平分∠BCD，将△ADC绕DC的中点旋转180°到△ECD处，B、C、E三点在同一直线上，∠B=2∠E．
    （1）求证：AB=DC；
    （2）若tanB=2，$AB=\sqrt{5}$，求四边形ABED的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某学校开运动会，要买一批笔记本和圆珠笔作为奖品，笔记本要买40苯，圆珠笔要买若干支，邱老师去了两家文具店，笔记本和圆珠笔的零售价分别为3元个2元，但甲文具店的营业员说：“若笔记本按零售价，则圆珠笔可按零售价的7折优惠．”乙文具店的营业员说：“笔记本和圆珠笔都可以按零售价的8折优惠．”
    （1）设要买的圆珠笔为x支，试用含x的式子表示甲、乙两个文具店的收费；
    （2）若学校要买80支圆珠笔作为奖品，你认为邱老师应取哪家文具店较合算？可节省多少钱？
    （3）要买圆珠笔y支时，选择甲文具店较合算，求此时节省多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，已知△ABC，点D在边BC上，点E在边AC上，点F在边AB上，且DE∥D1E1，EF∥E1F1，DF∥D1F1．求证：S△DEF•S△D1E1F1=S2△ABC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图将一张长方形纸片，分别沿着EP、FP对折，使点B落在点B′，点C落在C′．
    （1）若点P、B′、C′在同一直线上（如图1），求∠EPF的度数；
    （2）若点P，B′、C′不在同一直线上（如图2），且重叠部分∠B′PC′=12，求∠EPF；
    （3）若点P，B′，C′不在同一直线上（如图3），∠B′PC′=12，求∠EPF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，已知三角形纸片ABC中，AH⊥BC于H，将纸片沿AH折叠，点B落到BC上的点D处，再沿过点D线DE折叠，如果点C恰好落在点A处．那么下列结论中：①AB=CD；②AB+BH=CH；③∠ADH=∠ADE；④若△ABD的周长是28，△ABC的周长是44，则AC=16，正确的有①②④（填序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，两根木棒直立于桶底水平的木桶中，在桶中加入水后，一根在水下面的长度是它的总长度的$\frac{3}{4}$，另一根在水下面的长度是它的总长度的$\frac{4}{5}$．两根木棒的长度之和为62cm，求此时木桶中水的深度．

    查看答案和解析>>

    同步练习册答案