
 如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC.
如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC. 分析 根据平行线的性质和位似变换的概念得到△DEF与△D1E1F1是位似图形,设△DEF与△D1E1F1的相似比为$\frac{1}{k}$,△DEF的面积为1,表示出△D1E1F1面积,根据相似三角形的对应高的比等于相似比得到$\frac{OS}{OS+BT}$=$\frac{DF}{{D}_{1}{F}_{1}}$=$\frac{1}{k}$,结合图形解答即可.
解答 证明: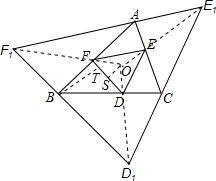 ∵DE∥D1E1,EF∥E1F1,DF∥D1F1,
∵DE∥D1E1,EF∥E1F1,DF∥D1F1,
∴△DEF与△D1E1F1是位似图形,即△DEF∽△D1E1F1,
∴E1E、F1F、D1D的延长线相交于点O,
作OS⊥DF于S,BT⊥DF于T,
设△DEF与△D1E1F1的相似比为$\frac{1}{k}$,△DEF的面积为1,
则△D1E1F1的面积为k2,
∴S△DEF•S△D1E1F1=k2,
∵DF∥D1F1,
∴△OFD∽△OF1D1,
∴$\frac{OS}{OS+BT}$=$\frac{DF}{{D}_{1}{F}_{1}}$=$\frac{1}{k}$,
∴$\frac{{S}_{△OFD}}{{S}_{四边形OFBD}}$=$\frac{1}{k}$,
同理,$\frac{{S}_{△ODE}}{{S}_{四边形ODCE}}$=$\frac{1}{k}$,$\frac{{S}_{△OEF}}{{S}_{四边形OEAF}}$=$\frac{1}{k}$,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=$\frac{1}{k}$,
∴S△ABC=k,
∴S△DEF•S△D1E1F1=S2△ABC.
点评 本题考查的是三角形的面积及等积变换,掌握相似三角形的判定定理和性质定理、位似变换的性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
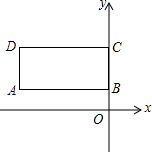 如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5.
如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.
如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,设A B,C,D是四个养猪场,现要建一座饲料加工厂,并且饲料加工厂到A,B,C,D各修-条公路.小明的爸爸承包了这项工程,为了节省资金,他请同学们给他设计道路施工方案.
如图所示,设A B,C,D是四个养猪场,现要建一座饲料加工厂,并且饲料加工厂到A,B,C,D各修-条公路.小明的爸爸承包了这项工程,为了节省资金,他请同学们给他设计道路施工方案.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
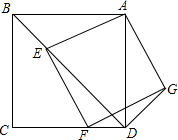 如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,
如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
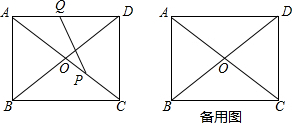 如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).
如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com