
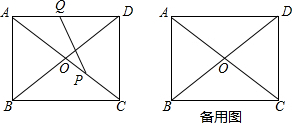
 如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).
如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).分析 (1)根据勾股定理得出AC=5,进而得出OB的长度;
(2)根据相似三角形的判定和性质进行解答即可;
(3)分三种情况利用相似三角形的判定和性质进行解答;
(4)分点P、Q在不同位置,根据等腰三角形的性质解答出x的值即可.
解答 解:(1)∵在矩形ABCD中,AD=4,DC=3,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}=\sqrt{{4}^{2}+{3}^{2}}=5$,
∴BO=$\frac{5}{2}$,
故答案为:$\frac{5}{2}$,
(2)如图1: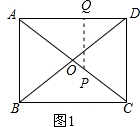 ∵PQ∥CD,
∵PQ∥CD,
∴△APQ∽△ACD,
∴$\frac{AQ}{AD}=\frac{AP}{AC}$,
∴$\frac{x}{4}=\frac{5-x}{5}$,
∴$x=\frac{20}{9}$;
(3)如图2,当$\frac{5}{2}≤x≤4$时,过点P作PE⊥AD,垂足为点E,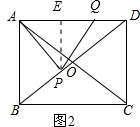 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠BAD=∠PED=90°,
∴PE∥AB,
∴△DPE∽△DBA,
∴$\frac{PE}{AB}=\frac{DP}{DB}$,
∴$\frac{PE}{3}=\frac{x}{5}$,
∴PE=$\frac{3}{5}x$,
∴${S}_{△APQ}=\frac{1}{2}•AD•PE=\frac{1}{2}x•\frac{3}{5}x=\frac{3}{10}{x}^{2}$,
∴$y=\frac{3}{10}{x}^{2}$,
如图3,当4<x≤5时,过点P作PF⊥AB,垂足为点F,延长FP交CD于点G,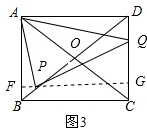 则PF∥AD,
则PF∥AD,
∵△BPF∽△BDA,
∴$\frac{PF}{AD}=\frac{BP}{BD}$,
∴$\frac{PF}{4}=\frac{5-x}{5}$,
∴$PF=\frac{4}{5}(5-x)=4-\frac{4}{5}x$,
∴$PG=\frac{4}{5}x$,
∴S四边形PQCB=S△BCD-S△PQD=$\frac{1}{2}CD•BC-\frac{1}{2}DQ•PG=\frac{1}{2}×3×4-\frac{1}{2}×\frac{4}{5}x(x-4)=-\frac{2}{5}{x}^{2}+\frac{8}{5}x+6$,
∴$y=\frac{2}{5}{x}^{2}+\frac{8}{5}x+6$;
∴S△APQ=S矩形ABCD-S△ABP-S△ADQ-S四边形PQCB
=$3×4-\frac{1}{2}×3(4-\frac{4}{5}x)-\frac{1}{2}×4(x-4)-(-\frac{2}{5}{x}^{2}+\frac{8}{5}x+6)$
=$\frac{2}{5}{x}^{2}-\frac{12}{5}x+8$,
∴$y=\frac{2}{5}{x}^{2}-\frac{12}{5}x+8$;
如图4,当5<x≤7时,过点Q作QH⊥AB,垂足为点H,则QH=AD=4,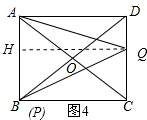 ∴${S}_{△APQ}=\frac{1}{2}•AB•QH=\frac{1}{2}×3×4=6$,
∴${S}_{△APQ}=\frac{1}{2}•AB•QH=\frac{1}{2}×3×4=6$,
∴S=6,
综上所述$y=\left\{\begin{array}{l}{\frac{3}{10}{x}^{2}(\frac{5}{2}≤x≤4)}\\{\frac{2}{5}{x}^{2}-\frac{12}{5}x+8(4<x≤5)}\\{6(5<x≤7)}\end{array}\right.$,
(4)AQ=PQ,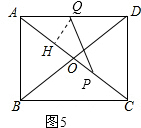
当点P在OC上时,如图5,作QH⊥AC于H,
则AH=HQ,△AHQ∽△ADC,
∴$\frac{AH}{AQ}$=$\frac{AD}{AC}$=$\frac{4}{5}$,
∵AQ=CP=x,
∴AH=$\frac{4}{5}$x,
∴$\frac{4}{5}$x+$\frac{4}{5}$x+x=5,
解得,x=$\frac{25}{13}$;
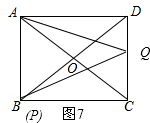
当Q与D重合时,如图6,AQ=4,QP=4,
∴x=4时,AQ=PQ;
当点P停止运动,Q运动到CD的中点时,如图7,
AQ=PQ,则△ADQ≌△BCQ,
∴DQ=QC,
∴AQ=$\frac{11}{2}$,
此时,x=$\frac{11}{2}$,
∴$x=\frac{25}{13},x=4,x=\frac{11}{2}$时,AQ=PQ.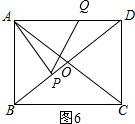
点评 此题考查的是四边形综合题,涉及的知识有:矩形的性质,相似三角形的判定与性质,利用了数形结合及分类讨论的数学思想,分类讨论时要做到不重不漏,考虑问题要全面.


科目:初中数学 来源: 题型:填空题
 如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°.
如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC.
如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
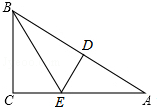 如图,已知Rt△ABC中,∠C=90°. 将△ABC沿BE折叠,使点C落在AB上的D处,折痕为BE.
如图,已知Rt△ABC中,∠C=90°. 将△ABC沿BE折叠,使点C落在AB上的D处,折痕为BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com