
 如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°.
如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°. 分析 先依据三角形的内角和定理求得∠A=60°,从而得到∠ADE+∠AED=120°,由翻折的性质可知∠ADF+∠AEF=240°,最后根据∠BDF+∠CEF=360°-(∠ADF+∠AEF)求解即可.
解答 解:∵在△ABC中,∠A=180°-∠B-∠C=60°,
∴∠ADE+∠AED=180°-∠A=120°.
由翻折的性质可知:∠ADE=∠FDE,∠AED=∠FED.
∴∠ADF+∠AEF=2(∠ADE+∠AED)=240°.
∴∠BDF+∠CEF=360°-(∠ADF+∠AEF)=360°-240°=120°.
故答案为:120°.
点评 本题主要考查的是翻折的性质,三角形的内角和定理,翻折的性质求得∠ADF+∠AEF=240°是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
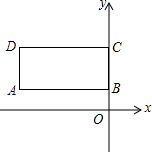 如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5.
如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.
如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
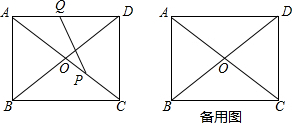 如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).
如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com