
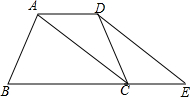
 如图,在梯形ABCD中,AD∥BC,CA平分∠BCD,将△ADC绕DC的中点旋转180°到△ECD处,B、C、E三点在同一直线上,∠B=2∠E.
如图,在梯形ABCD中,AD∥BC,CA平分∠BCD,将△ADC绕DC的中点旋转180°到△ECD处,B、C、E三点在同一直线上,∠B=2∠E.分析 (1)证明∠DCB=2∠E,则∠B=∠DCB,则可以证明梯形ABCD是等腰梯形,据此即可证得;
(2)过点A作AF⊥BC于F,在直角△ABF中,利用三角函数即可求得AF的长和BF的长,然后证明AD=DC=AB,则BC的长即可求得,然后利用梯形的面积公式即可求解.
解答 (1)证明:∵CA平分∠BCD,
∴∠BCD=2∠ACB,
∴∠DAC=∠ACB,
∴∠ACB=∠CAD.
∵将△ADC绕DC的中点旋转180°到△ECD处,
∴∠E=∠CAD,
又∵在梯形ABCD中,∠DAC=∠ACB,
∴2∠E=2∠ACB=∠BCD,
∵∠B=2∠E,
∴∠B=∠BCD.
∴AB=CD;
(2)过点A作AF⊥BC于F,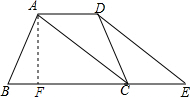
∵tanB=2,
∴AF:BF=2,AF2+BF2=AB2,
∵$AB=\sqrt{5}$,
∴AF=2,BF=1.
∵CA平分∠BCD,
∴∠BCD=∠ACD,
∴∠DAC=∠ACB,
∴∠ACB=∠CAD,
∴∠ACD=∠CAD,
∴AD=DC 由(1)知AB=CD,
∴AB=CD=AD=$\sqrt{5}$,
∴BC=2+$\sqrt{5}$.
∵将△ADC绕DC的中点旋转180°到△ECD处,B、C、E三点在同一直线上,
∴BE=2+2$\sqrt{5}$,
∴四边形ABED的面积为2+3$\sqrt{5}$.
点评 本题考查了梯形的性质以及旋转的性质,正确作出辅助线,正确证明梯形ABCD是等腰梯形是本题的关键.


科目:初中数学 来源: 题型:解答题
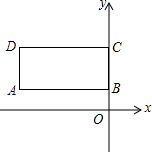 如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5.
如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.
如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,设A B,C,D是四个养猪场,现要建一座饲料加工厂,并且饲料加工厂到A,B,C,D各修-条公路.小明的爸爸承包了这项工程,为了节省资金,他请同学们给他设计道路施工方案.
如图所示,设A B,C,D是四个养猪场,现要建一座饲料加工厂,并且饲料加工厂到A,B,C,D各修-条公路.小明的爸爸承包了这项工程,为了节省资金,他请同学们给他设计道路施工方案.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com