
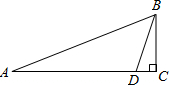
 如图,一艘军舰从点A向位于正东方向的C岛航行,在点A处测得B岛在其北偏东60°方向,航行75海里到达点D处,测得B岛在其北偏东30°,继续航行5千米到达C岛,此时接到通知,要求这艘军舰在半小时内赶到正北方向的B岛执行任务,则这艘军舰航行速度至少为多少才能按时赶到B岛?
如图,一艘军舰从点A向位于正东方向的C岛航行,在点A处测得B岛在其北偏东60°方向,航行75海里到达点D处,测得B岛在其北偏东30°,继续航行5千米到达C岛,此时接到通知,要求这艘军舰在半小时内赶到正北方向的B岛执行任务,则这艘军舰航行速度至少为多少才能按时赶到B岛? 分析 首先在AC上取点E,作AE=BE,易求得∠BEC=60°,然后设AE=x海里,可求得BE=AE=x海里,EC=x海里,则可得方程x+x=75+5,继而求得答案.
解答 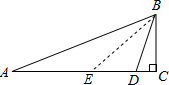 解:在AC上取点E,作AE=BE,
解:在AC上取点E,作AE=BE,
∵∠A=30°,
∴∠ABE=∠A=30°,
∴∠BEC=∠A+∠ABE=60°,
设AE=x,
则BE=AE=x,
在Rt△BEC中,EC=BE•cos60°=x,
∵AD=75千米,CD=5千米,
∴x+$\frac{1}{2}$x=75+5,
解得:x=$\frac{160}{3}$,
∴BE=$\frac{160}{3}$(千米),
∴BC=$\frac{\sqrt{3}}{2}$BE=$\frac{80\sqrt{3}}{3}$(千米),
∵这艘军舰在半小时内赶到正北方向的B岛执行任务,
∴$\frac{80\sqrt{3}}{3}$÷$\frac{1}{2}$=$\frac{160\sqrt{3}}{3}$(千米/时),
∴这艘军舰航行速度至少为$\frac{160\sqrt{3}}{3}$千米/时时才能按时赶到B岛.
点评 此题考查了方向角问题.此题难度适中,注意构造直角三角形,并利用解直角三角形的知识求解;注意数形结合思想与方程思想的应用.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com