
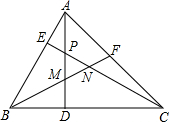
 如图所示,△ABC中,∠ABC=60°,∠BAC=75°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD与CE相交于点P,∠ABC的平分线BF分别交AD、CE、AC于点M、N、F.
如图所示,△ABC中,∠ABC=60°,∠BAC=75°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD与CE相交于点P,∠ABC的平分线BF分别交AD、CE、AC于点M、N、F.分析 (1)由已知条件,根据三角形内角和等于180、角的平分线的性质求得各个角的度数,然后利用等腰三角形的判定进行找寻,注意做到由易到难.
(2)BM=2MD,AM=BM,则AD=3ND=6cm,易证DC=AD=6cm.
解答 解:(1)△ADC,△AMB,△BNC,△MNP,△ABF.理由如下:
∵∠ABC=60°,∠BAC=75°,AD,CF分别是BC,AB边上的高
∴∠DAC=45°,
又∵∠ACB=45°
∴△ADC为等腰三角形.
∵∠ABC的平分线BE分别交AD,CF于M,N
∴∠ABM=30°,
又∵∠BAM=30°
∴△AMB为等腰三角形.
由题意可知∵∠NBC=∠NCB=30°
∴△BNC为等腰三角形.
∠PMN=∠MNP=60°
∴△MNP为等腰三角形.
∵∠ABF=30°,∠BAC=75°
∴∠BFA=75°
∴△ABF为等腰三角形.
(2)∵∠ABC=60°,AD⊥BC,
∴∠BAD=30°,
∵BF平分∠ABC
∴∠ABM=∠DBM=30°,
∴∠ABM=∠BAD=30°,
∴AM=BM=2DM=4cm,
∴AD=AM+DM=4+2=6cm,
∵∠BAC=75°,
∴∠DAC=∠BAC-∠BAD=75°-30°=45°,△ACD为等腰直角三角形,
∴DC=AD=6cm.
点评 本题考查了等腰三角形的性质和判定、角的平分线的性质及三角形内角和定理;由已知条件利用相关的性质求得各个角的度数是正确解答本题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
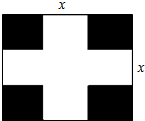 为了美化校园,学校在校内一块长30m,宽20m的长方形空地上修建如图所示的十字路(空白处),四个角铺上草坪(面积相等的小长方形的阴影部分).设十字路的宽为xm,则用整式表示草坪的面积为600-50x+x2m2.
为了美化校园,学校在校内一块长30m,宽20m的长方形空地上修建如图所示的十字路(空白处),四个角铺上草坪(面积相等的小长方形的阴影部分).设十字路的宽为xm,则用整式表示草坪的面积为600-50x+x2m2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
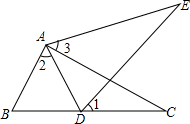 如图,点D在△ABC的边BC上,点E在△ABC的外部,且∠1=∠2=∠3,要使△ABC≌△ADE,还应添加的条件是如:AB=AD等,答案不唯一(写一种即可)
如图,点D在△ABC的边BC上,点E在△ABC的外部,且∠1=∠2=∠3,要使△ABC≌△ADE,还应添加的条件是如:AB=AD等,答案不唯一(写一种即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a-12)件 | B. | (2a+12)件 | C. | (2a-18)件 | D. | (2a+18)件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com