
【题目】如图,弓形ABC中,∠BAC=60°,BC=2![]() ,若点P在优弧BAC上由点B向点C移动,记△PBC的内心为I,点I随点P的移动所经过的路程为m,则m的取值范围为_____.
,若点P在优弧BAC上由点B向点C移动,记△PBC的内心为I,点I随点P的移动所经过的路程为m,则m的取值范围为_____.
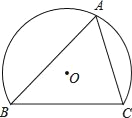
【答案】0<m<![]() .
.
【解析】
可设I为△PBC的内心连接BI,利用点I的轨迹是以点D为圆心,2为半径的弧CIB(不含点C、B),可求出弧CIB的长为![]() ,进而求出m的取值范围.
,进而求出m的取值范围.
如图,
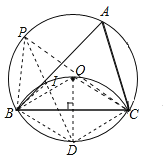
将圆补全,过点O作OD⊥BC交⊙O于点D,设I为△PBC的内心连接BI、连接PD、连接BO、连接CO、连接BD、连接CD、连接PB、连接PC,
∵DO⊥BC,
∴BD=CD,∠BPD=∠CPD,
∵PBI+∠BPI=∠BID,∠DBC+∠CBI=∠IBD,∠BPD=∠BCD,
∴∠DBI=∠BID,
∴ID=BD,
∵∠BAC=60°,BC=2![]() ,
,
∴∠BOD=60°,△BDO是等边三角形,
∴BO=![]() =2,
=2,
∴BD=BO=ID=2,
∴动点I到定点D的距离为2,即点I的轨迹是以点D为圆心,2为半径的弧CIB(不含点C、B),
弧CIB的长为![]() ,
,
则m的取值范围是0<m<![]() .
.
故答案为:0<m<![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】我市部分学生参加了全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
请根据以上信息解答下列问题:
(1)全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么分数范围?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩分数的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为105人”等等.请你再写出两条此表提供的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:P(4,1)为平面直角坐标系中的一点,点A(a,0),点B(0,a)(其中a>0)分别是坐标轴上的动点,若△PAB的面积为3,试求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于![]() cm2?
cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
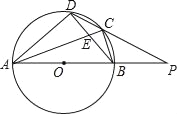
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
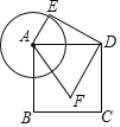
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,
(1)当∠EAD=90°时,AF=________________.
(2)在E的整个运动过程中,AF的最大值是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
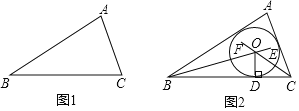
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:![]() 求作:
求作:![]() 的内切圆.
的内切圆.
小明的作法如下:如图2,
![]() 作
作![]() ,
,![]() 的平分线BE和CF,两线相交于点O;
的平分线BE和CF,两线相交于点O;
![]() 过点O作
过点O作![]() ,垂足为点D;
,垂足为点D;
![]() 点O为圆心,OD长为半径作
点O为圆心,OD长为半径作![]() 所以,
所以,![]() 即为所求作的圆.
即为所求作的圆.
请回答:该尺规作图的依据是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com