
【题目】在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,不能判断△ABC为直角三角形是( )
A.∠A︰∠B︰∠C=3︰4︰5B.![]() =1,
=1,![]() =2,
=2,![]() =3
=3
C.(b+c)(b-c)=![]() D.∠A-∠B=∠C
D.∠A-∠B=∠C
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】下列各式,能够表示图中阴影部分的面积的是( )
①ac+(b﹣c)c;②ac+bc﹣c2;③ab﹣(a﹣c)(b﹣c);④(a﹣c)c+(b﹣c)c+c2

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步
是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步![]() 小路的宽度不计
小路的宽度不计![]() 观测得点B在点A的南偏东
观测得点B在点A的南偏东![]() 方向上,点C在点A的南偏东
方向上,点C在点A的南偏东![]() 的方向上,点B在点C的北偏西
的方向上,点B在点C的北偏西![]() 方向上,AC间距离为400米
方向上,AC间距离为400米![]() 问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
![]() 参考数据:
参考数据:![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为t s.
(1)求CD的长;
(2)t为何值时,△ACP是等腰三角形?
(3)若M为BC上一动点,N为AB上一动点,是否存在M,N使得AM+MN 的值最小?如果有,请直接写出最小值,如果没有,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
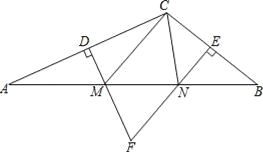
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 中,
中,![]() ,点E为AC上的一点,连接BE,在BC上找一点G,使得
,点E为AC上的一点,连接BE,在BC上找一点G,使得![]() ,AG交BE于K.
,AG交BE于K.
![]() 若
若![]() ,且
,且![]() ,
,![]() ,求EK的长度.
,求EK的长度.
![]() 如图2,过点A作
如图2,过点A作![]() 交BE于点D,过
交BE于点D,过![]() 分别向AB所在的直线作垂线,垂足分别为点M、N,且
分别向AB所在的直线作垂线,垂足分别为点M、N,且![]() ,若D为BE的中点,证明:
,若D为BE的中点,证明:![]()
![]() 如图3,将
如图3,将![]() 中的条件“若D为BE的中点”改为“若
中的条件“若D为BE的中点”改为“若![]() 是大于2的整数
是大于2的整数![]() ”,其他条件不变,请直接写出
”,其他条件不变,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com