
【题目】如图1,已知![]() 中,
中,![]() ,点E为AC上的一点,连接BE,在BC上找一点G,使得
,点E为AC上的一点,连接BE,在BC上找一点G,使得![]() ,AG交BE于K.
,AG交BE于K.
![]() 若
若![]() ,且
,且![]() ,
,![]() ,求EK的长度.
,求EK的长度.
![]() 如图2,过点A作
如图2,过点A作![]() 交BE于点D,过
交BE于点D,过![]() 分别向AB所在的直线作垂线,垂足分别为点M、N,且
分别向AB所在的直线作垂线,垂足分别为点M、N,且![]() ,若D为BE的中点,证明:
,若D为BE的中点,证明:![]()
![]() 如图3,将
如图3,将![]() 中的条件“若D为BE的中点”改为“若
中的条件“若D为BE的中点”改为“若![]() 是大于2的整数
是大于2的整数![]() ”,其他条件不变,请直接写出
”,其他条件不变,请直接写出![]() 的值.
的值.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,不能判断△ABC为直角三角形是( )
A.∠A︰∠B︰∠C=3︰4︰5B.![]() =1,
=1,![]() =2,
=2,![]() =3
=3
C.(b+c)(b-c)=![]() D.∠A-∠B=∠C
D.∠A-∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两个直角顶点![]() 叠放在一起(如图①),其中
叠放在一起(如图①),其中![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)试猜想![]() 与
与![]() 的数量关系,请说明理由;
的数量关系,请说明理由;
(3)若按住三角板![]() 不动,绕顶点
不动,绕顶点![]() 转动三角板
转动三角板![]() ,试探究
,试探究![]() 等于多少度时,
等于多少度时,![]() ,并简要说明理由.
,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市欲购进一种今年新上市的产品,购进价为20元![]() 件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量
件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量![]() 件
件![]() 与每件的销售价
与每件的销售价![]() 元
元![]() 件
件![]() 之间有如下关系:
之间有如下关系:![]()
![]() 请写出该超市销售这种产品每天的销售利润
请写出该超市销售这种产品每天的销售利润![]() 元
元![]() 与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
![]() 若超市想获取1500元的利润
若超市想获取1500元的利润![]() 求每件的销售价.
求每件的销售价.
![]() 若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点
经过点![]() 和点
和点![]()
![]() 求该抛物线所对应的函数解析式;
求该抛物线所对应的函数解析式;
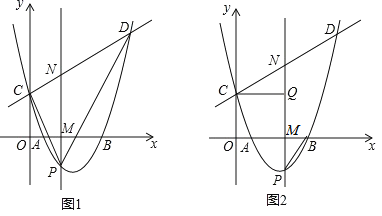
![]() 该抛物线与直线
该抛物线与直线![]() 相交于
相交于![]() 两点,点P是抛物线上的动点且位于x轴下方,直线
两点,点P是抛物线上的动点且位于x轴下方,直线![]() 轴,分别与x轴和直线CD交于点M、N.
轴,分别与x轴和直线CD交于点M、N.
①连结PC、PD,如图1,在点P运动过程中,![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
②连结PB,过点C作![]() ,垂足为点Q,如图2,是否存在点P,使得
,垂足为点Q,如图2,是否存在点P,使得![]() 与
与![]() 相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距200km的A,B两地同时出发,它们离A地的距离s(km)随时间t(h)变化的图象如图所示,则下列结论:①甲车的平均速度为40km/h,②乙车行驶3h到达A地,稍作停留后返回B地,③经![]() h后,两车在途中相遇,④乙车返回B地的平均速度比去A地的平均速度大,其中正确的有________________________(填序号)
h后,两车在途中相遇,④乙车返回B地的平均速度比去A地的平均速度大,其中正确的有________________________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽君花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(2)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少总费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com