
����Ŀ���ڡ�ABC�У���P��ƽ��������һ�㣨��ͬ��A��B��C��������P��A��B��C�е�ij��������ߵļн�Ϊֱ��ʱ����Ƶ�PΪ��ABC��һ�����ɵ�.

��1����ͼ1������P�ǡ�ABC��һ�㣬��A=55�㣬��ABP=10�㣬��ACP=25�㣬��˵����P�ǡ�ABC��һ�����ɵ㣻
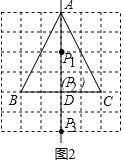
��2����ͼ2��������ABC�Ķ��㶼�ڸ���ϣ���D��BC���е㣬��P��ֱ��AD�ϣ�����ͼ�б��ʹ�õ�P�ǡ�ABC�Ĺ��ɵ�ʱ����P��λ�ã�
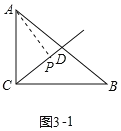
��3����Rt��ABC�У���ACB=90�㣬AC=12��BC=16����D��AB���е㣬��P������CD��.����P�ǡ�ABC�Ĺ��ɵ㣬�����CP�ij���
���𰸡���1����������(2)��������(3)7.2��12.8��20��
��������
��1�������������ڽǺͶ�����֤�á�CPB��90�����ɣ�
��2�����������ص��Լ����ɵ�Ķ�����н�ɣ�
��3����������ۣ��١�APC��90��ʱ���ڵ���CPB��90��ʱ���۵���APB��90��ʱ���ֱ���⼴�ɣ�
�⣺��1������ABC�У���A��55����
���ACB+��ABC��125����
�ߡ�ACP��10������ABP��25����
���PCB+��PBC��90����
���CPB��90����
���P����ABC��һ�����ɵ㣮
��2����ͼ����P1��P2��P3��Ϊ����
��3����Rt��ABC����ACB��90����AC��12��BC��16��
��AB��20��
�֡ߵ�D��AB���е㣬
��AD��BD��CD��10��
�١�APC��90��ʱ����CP��x��DP��10��x��
��Rt��APC��Rt��APD��
��AC2��CP2��AD2��DP2������122��x2��102����10��x��2��
��ã�x��7.2��
�ڵ���CPB��90��ʱ����CP��x��DP��x��10��

��Rt��BPD��Rt��BPC����BC2��CP2��BD2��DP2����162��x2��102����x��10��2��
��ã�x��12.8��
�۵���APB��90��ʱ��

��Rt��APB��DP��![]() AB��10��
AB��10��
��CP��20
����������CP�ij�Ϊ7.2��12.8��20��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ�����ͼ����A��3��3����B��4��0����ԭ��O��PΪ���κ���ͼ���ϵ�һ�����㣬����P��x��Ĵ��ߣ�����ΪD��m��0��������ֱ��OA���ڵ�C��
��1����ֱ��OA�Ͷ��κ����Ľ���ʽ��
��2������P��ֱ��OA���Ϸ�ʱ��
�ٵ�PC�ij����ʱ�����P�����ꣻ
�ڵ�S��PCO=S��CDOʱ�����P�����꣮
 ��������
��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���ABC��ƽ�������ڡ�ACE��ƽ�����ཻ�ڵ�D����֪��ABC=70������ACB=30�������A�͡�D�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�������ı���ABCD�У�AB��CD����B=90�㣬��P��BC���ϣ�����APD=90��ʱ����֪��ABP�ס�PCD������Ҫ��֤����
̽������ͼ�������ı���ABCD�У���P��BC���ϣ�����B=��C=��APDʱ����֤����ABP�ס�PCD��
��չ����ͼ��������ABC�У���P�DZ�BC���е㣬��D��E�ֱ��ڱ�AB��AC�ϣ�����B=��C=��DPE=45�㣬BC=6![]() ��CE=4����DE�ij�Ϊ�� ����
��CE=4����DE�ij��� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�������̶�����һ��ǽ��ǽ�ij��Ȳ��ޣ�����40�׳������Χ��һ�������εIJֿ⣮
��1�����ε������150ƽ���ף�������������ڱߵij���
��2���ܷ�Χ�����220ƽ���ij����Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Rt��ABC�У���BAC��90����AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE��AF����DF��DN����AE��CN���ܡ�AMD�͡�DMN�������ȣ����д���Ľ��۸����ǣ�������

A.3��B.2��C.1��D.0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪��O�DZ�AB��AC��ֱƽ���ߵĽ��㣬��E�ǡ�ABC����ACB��ƽ���ߵĽ��㣬����O+��E��180�������A��_____�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����B��6��0����ֱ��AB��ֱ��OA�ཻ�ڵ�A��4��2����

��1����ֱ��AB�ĺ�������ʽ��
��2������y���ϴ���һ��M��ʹMA+MB��ֵ��С���������M�����ꣻ
��3����x�����Ƿ���ڵ�N��ʹ��AON�ǵ��������Σ�������ڣ�ֱ��д����N�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �����
�����![]() ��ƽ���߽�
��ƽ���߽�![]() �ߵĴ�ֱƽ�����ڵ�
�ߵĴ�ֱƽ�����ڵ�![]() .
.![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() .
.
��1����֤��![]()
��2����![]() ��
��![]() ����
����![]() �ij�
�ij�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com